
【题目】如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EB.若AB=8,CD=2.
(1) 求⊙O半径OA的长;
(2) 求EB的长.

【答案】(1)5;(2)6
【解析】(1)⊙O的半径OD⊥弦AB于点C,AB=8,根据垂径定理得到AC=![]() AB=4,设⊙O的半径为r,则OC=r-2,在Rt△AOC中,根据勾股定理即可求出求⊙O半径OA的长;
AB=4,设⊙O的半径为r,则OC=r-2,在Rt△AOC中,根据勾股定理即可求出求⊙O半径OA的长;
(2)AE是⊙O的直径,根据圆周角定理得到∠ABE=90°,在Rt△ABE中,用勾股定理即可求得EB的长.
(1)∵⊙O的半径OD⊥弦AB于点C,AB=8,

∴AC=![]() AB=4,
AB=4,
设⊙O的半径为r,则OC=r-2,
在Rt△AOC中,
∵AC=4,OC=r-2,
∴OA2=AC2+OC2,即r2=42+(r﹣2)2,解得r=5,
∴⊙O半径OA的长为5.
(2)∵AE是⊙O的直径,
∴∠ABE=90°,
在Rt△ABE中,
∵AE=10,AB=8,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】综合与探究
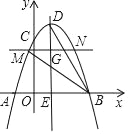
如图,抛物线y=﹣![]() x2+2x+6与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,其对称轴与抛物线交于点D.与x轴交于点E.
x2+2x+6与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,其对称轴与抛物线交于点D.与x轴交于点E.
(1)求点A,B,D的坐标;
(2)点G为抛物线对称轴上的一个动点,从点D出发,沿直线DE以每秒2个单位长度的速度运动,过点C作x轴的平行线交抛物线于M,N两点(点M在点N的左边).
设点G的运动时间为ts.
①当t为何值时,以点M,N,B,E为顶点的四边形是平行四边形;
②连接BM,在点G运动的过程中,是否存在点M.使得∠MBD=∠EDB,若存在,求出点M的坐标;若不存在,请说明理由;
(3)点Q为坐标平面内一点,以线段MN为对角线作萎形MENQ,当菱形MENQ为正方形时,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年11月铜陵举办了国际半程马拉松比赛,吸引了大批运动爱好者.某商场看准时机,想订购一批![]() 款运动鞋,现有甲,乙两家供应商,它们均以每双
款运动鞋,现有甲,乙两家供应商,它们均以每双![]() 元的价格出售
元的价格出售![]() 款运动鞋,其中供应商甲一律九折销售, 与购买数量无关;而供应商乙规定:购买数量在
款运动鞋,其中供应商甲一律九折销售, 与购买数量无关;而供应商乙规定:购买数量在![]() 双以内(包含
双以内(包含![]() 双),以每双200元的原价出售,当购买数量超出
双),以每双200元的原价出售,当购买数量超出![]() 双时,其超出部分按原价的八折出售.问:
双时,其超出部分按原价的八折出售.问:
![]() 某商场购买多少双时,去两个供应商处的进货价钱一样多?
某商场购买多少双时,去两个供应商处的进货价钱一样多?
![]() 若该商场分两次购买运动鞋,第一次购进
若该商场分两次购买运动鞋,第一次购进![]() 双,第二次购进的数量是第次的
双,第二次购进的数量是第次的![]() 倍多
倍多![]() 双,如果你是商场经理,在两次分开购买的情况下,你预计花多少元采购运动鞋,才能使得商场花销最少?
双,如果你是商场经理,在两次分开购买的情况下,你预计花多少元采购运动鞋,才能使得商场花销最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图并填空,如图:方格纸中每个小正方形的边长都为1,△ABC的顶点都在方格纸的格点上,将△ABC经过一次平移后得到△A'B'C'.图中标出了点C的对应点C'.
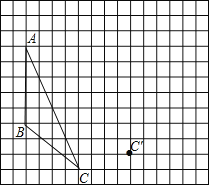
(1)请画出平移后的△A'B'C';
(2)若连接AA',BB',则这两条线段的关系是 ;
(3)利用网格画出△ABC中AC边上的中线BD以及AB边上的高CE;
(4)线段AB在平移过程中扫过区域的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠BAC=90°时,那么∠DCE= 度;
(2)设∠BAC= ![]() ,∠DCE=
,∠DCE= ![]() .
.
① 如图2,当点D在线段CB上,∠BAC≠90°时,请你探究![]() 与
与![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
② 如图3,当点D在线段CB的延长线上,∠BAC≠90°时,请将图3补充完整,并直接写出此时![]() 与
与![]() 之间的数量关系(不需证明).
之间的数量关系(不需证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利, 尽快减少库存,商场决定采取适当的降价措施.假设在一定范围内,衬衫的单价每降低1元,商场平均每天可多售出2件.设衬衫的单价降了x元:
(1)该商场降价后每件盈利___________元,每天可售出________件;
(2)如果商场通过销售这批衬衫每天盈利1200元,那么衬衫的单价降了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠ABC=90°,D是直线AB边上的点,AD=BC
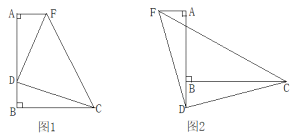
(1)如图1,点D在线段AB上,过点A作AF⊥AB,且AF=BD,连接DC、DF、CF,试判断△CDF的形状并说明理由;
(2)如图2,点D在线段AB的延长线上,点F在点A的左侧,其他条件不变,以上结论是否仍然成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知整数a1,a2,a3,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…依此类推,则a2020的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.
(1)求证:直线CE是⊙O的切线.
(2)若BC=3,CD=3![]() ,求弦AD的长.
,求弦AD的长.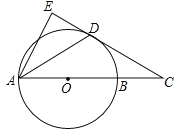
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com