
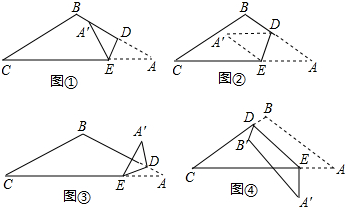
 解:(1)如图1,∠CEA′=2∠A.
解:(1)如图1,∠CEA′=2∠A.

科目:初中数学 来源: 题型:
 我国古代数学家赵爽的“勾股方圆图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是25,小正方形的面积是1,直角三角形的两直角边分别是a和b,那么(a+b)2的值为
我国古代数学家赵爽的“勾股方圆图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是25,小正方形的面积是1,直角三角形的两直角边分别是a和b,那么(a+b)2的值为查看答案和解析>>
科目:初中数学 来源: 题型:
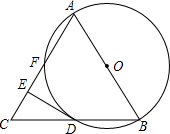 如图,△ABC中,AB=AC,以AB为直径的⊙O,交BC于D点交AC于F点,过点D作DE⊥AC,垂足为E.
如图,△ABC中,AB=AC,以AB为直径的⊙O,交BC于D点交AC于F点,过点D作DE⊥AC,垂足为E. |
| BD |
 |
| DF |
 |
| DF |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC是边长为4cm的等边三角形,P是△ABC内的任意一点,过点P作EF∥AB分别交AC,BC于点E,F,作GH∥BC分别交AB,AC于点G,H,作MN∥AC分别交AB,BC于点M,N,试猜想:EF+GH+MN的值是多少?其值是否随P位置的改变而变化?并说明你的理由.
如图,△ABC是边长为4cm的等边三角形,P是△ABC内的任意一点,过点P作EF∥AB分别交AC,BC于点E,F,作GH∥BC分别交AB,AC于点G,H,作MN∥AC分别交AB,BC于点M,N,试猜想:EF+GH+MN的值是多少?其值是否随P位置的改变而变化?并说明你的理由.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、y=-2(x+1)2-2 |
| B、y=-2(x+1)2+2 |
| C、y=-2(x-1)2-2 |
| D、y=-2(x-1)2+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| y |
| 1 |
| x |
| 1 |
| a |
| 1 |
| b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com