
分析 (1)移项后配方即可解答;
(2)分别解出两个不等式的解集,再求出其公用部分.
解答 解:(1)解方程x2-4x+1=0,
移项得,x2-4x=-1,
配方得,x2-4x+4=-1+4,
(x-2)2=3,
开方得,x-2=±$\sqrt{3}$,
解得,x=2±$\sqrt{3}$,
x1=2+$\sqrt{3}$,x2=2-$\sqrt{3}$.
(2)$\left\{\begin{array}{l}x-3(x+2)≥2①\\ x-1<\frac{2+x}{4}②\end{array}\right.$,
由①得,x≤-4,
由②得,x<2,
则不等式组的解集为x≤-4.
点评 (1)本题考查了解一元二次方程--配方法,配方法的一般步骤:
①把常数项移到等号的右边;
②把二次项的系数化为1;
③等式两边同时加上一次项系数一半的平方.
选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.
(2)本题考查了解一元一次不等式组,熟悉不等式的解法是解题的关键.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
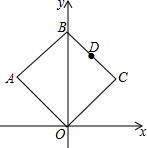 如图,正方形OABC的对角线OB在y轴正半轴上,且OB=4,点A在第二象限,点C在第一象限,点D是BC的中点,则点D的坐标是(1,3).
如图,正方形OABC的对角线OB在y轴正半轴上,且OB=4,点A在第二象限,点C在第一象限,点D是BC的中点,则点D的坐标是(1,3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
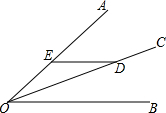 如图,D是∠AOB平分线OC上一点,过点D作DE∥OB交射线OA于点E,已知∠BOD=25°,则∠OED=( )
如图,D是∠AOB平分线OC上一点,过点D作DE∥OB交射线OA于点E,已知∠BOD=25°,则∠OED=( )| A. | 40° | B. | 50° | C. | 130° | D. | 150° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
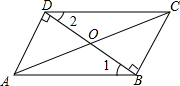 如图,△ABD和△CDB是两块形状、大小相同的三角尺,它们较长的直角边靠在一起(即重合在线段BD上),∠1=∠2=30°,∠ADB=∠CBD=90°,AD=8$\sqrt{3}$cm,连接AC,AC与BD相交于O点.求AC的长度.
如图,△ABD和△CDB是两块形状、大小相同的三角尺,它们较长的直角边靠在一起(即重合在线段BD上),∠1=∠2=30°,∠ADB=∠CBD=90°,AD=8$\sqrt{3}$cm,连接AC,AC与BD相交于O点.求AC的长度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com