练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

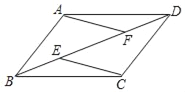
    【题目】已知：如图，E、F是平行四边形ABCD的对角线BD上的两点，BE＝DF．

    求证：（1）△ADF≌△CBE；

    （2）CE∥AF．

    【答案】(1)见解析;(2)见解析.

    【解析】

    （1）根据平行四边形的性质得到AD=BC，AD∥BC，由平行线的性质得到∠ADF=∠CBE，利用SAS证明即可；

    （2）根据全等三角形的性质得到∠AFD=∠CEB，根据等角的补角相等得到∠AFB=∠CED，根据平行线的判定定理证明CE∥AF．

    （1）∵四边形ABCD是平行四边形，∴AD=BC，AD∥BC，∴∠ADF=∠CBE．

    在△ADF和△CBE中，∵AD=BC，∠ADF=∠CBE，BE=DF，∴△ADF≌△CBE；

    （2）∵△ADF≌△CBE，∴∠AFD=∠CEB，∴∠AFB=∠CED，∴CE∥AF．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】济南某中学在参加“创文明城，点赞泉城”书画比赛中，杨老师从全校30个班中随机抽取了4个班（用A，B，C，D表示），对征集到的作鼎的数量进行了分析统计，制作了两幅不完整的统计图．

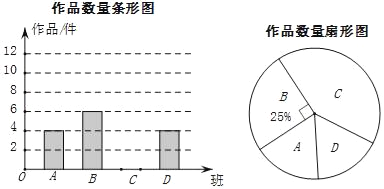
    请根据以上信息，回答下列问题：

    （l）杨老师采用的调查方式是　 　（填“普查”或“抽样调查”）；

    （2）请补充完整条形统计图，并计算扇形统计图中C班作品数量所对应的圆心角度数　 　．

    （3）请估计全校共征集作品的什数．

    （4）如果全枝征集的作品中有5件获得一等奖，其中有3名作者是男生，2名作者是女生，现要在获得一样等奖的作者中选取两人参加表彰座谈会，请你用列表或树状图的方法，求恰好选取的两名学生性别相同的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

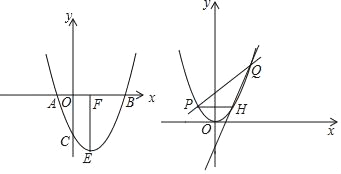
    【题目】抛物线y＝x2+bx+c经过点A、B、C，已知A（﹣1，0），C（0，﹣3）．

    （1）求抛物线的解析式；

    （2）如图1，抛物线顶点为E，EF⊥x轴于F点，M（m，0）是x轴上一动点，N是线段EF上一点，若∠MNC＝90°，请指出实数m的变化范围，并说明理由．

    （3）如图2，将抛物线平移，使其顶点E与原点O重合，直线y＝kx+2（k＞0）与抛物线相交于点P、Q（点P在左边），过点P作x轴平行线交抛物线于点H，当k发生改变时，请说明直线QH过定点，并求定点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

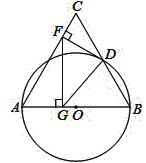
    【题目】如图，已知等边△ABC，以AB为直径的圆与BC边交于点D，过点D作DF⊥AC，垂足为F，过点F作FG⊥AB，垂足为G，连结GD．

    （1）求证：DF是⊙O的切线；

    （2）若AB＝12，求FG的长；

    （3）在（2）问条件下，求点D到FG的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

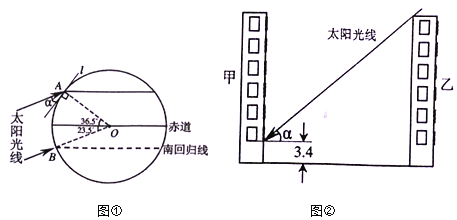
    【题目】图①，②是晓东同学在进行“居民楼高度、楼间距对住户采光影响问题”的研究时画的两个示意图.请你阅读相关文字，解答下面的问题.

    （1）图①是太阳光线与地面所成角度的示意图.冬至日正午时刻，太阳光线直射在南回归线（南纬23.5）B地上.在地处北纬36.5的A地，太阳光线与地面水平线l所成的角为，试借助图①，求的度数.

    （2）图②是乙楼高度、楼间距对甲楼采光影响的示意图.甲楼地处A地，其二层住户的南面窗户下沿距地面3.4米.现要在甲楼正南面建一幢高度为22.3米的乙楼，为不影响甲楼二层住户（一层为车库）的采光，两楼之间的距离至少应为多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

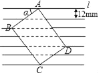
    【题目】如图，把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中，恰好四个顶点都在横格线上．已知α=36°，求长方形卡片的周长．

    （精确到1mm，参考数据：sin36°≈0.60，cos36°≈0.80，tan36°≈0.75）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有一张矩形纸片ABCD，，．

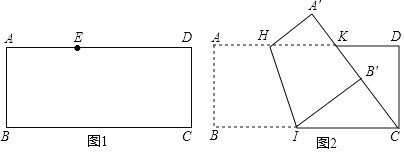
    如图1，点E在这张矩形纸片的边AD上，将纸片折叠，使AB落在CE所在直线上，折痕设为点M，N分别在边AD，BC上，利用直尺和圆规画出折痕不写作法，保留作图痕迹；

    如图2，点K在这张矩形纸片的边AD上，，将纸片折叠，使AB落在CK所在直线上，折痕为HI，点A，B分别落在点，处，小明认为所在直线恰好经过点D，他的判断是否正确，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2020年东京奥运会的比赛门票开始接受公众预订．下表为奥运会官方票务网站公布的几种球类比赛的门票的人民币价格，球迷小李用12000元做为预订下表中比赛项目门票的资金．

    比赛项目

    票价(元／场)

    男篮

    1000

    足球

    800

    乒乓球

    500

    (1)若全部资金用来预订男篮门票和乒乓球门票共15张，问男篮门票和乒乓球门票各订多少张?

    (2)若在准备资金允许的范围内和总票数不变的前提下，这个球迷想预定上表中三种球类门票，其中足球门票与乒乓球门票数相同，且足球门票的费用不超过男篮门票的费用，问可以预订这三种球类门票各多少张？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

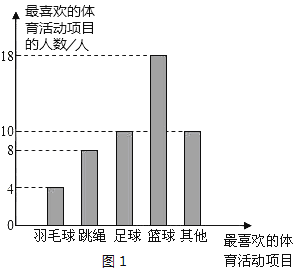
    【题目】某校围绕着“你最喜欢的体育活动项目是什么？（只写一项）”的问题，对在校学生进行了随机抽样调查，从而得到一组数据，如图1是根据这组数据绘制的条形统计图，请结合统计图回答下列问题：

    （1）该校对多少名学生进行了抽样调查？

    （2）本次抽样调查中，最喜欢足球活动的有多少人？占被调查人数的百分比是多少？

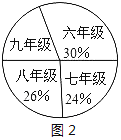
    （3）若该校九年级共有400名学生，图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图，请你估计全校学生中最喜欢篮球活动的人数约为多少？

    查看答案和解析>>

    同步练习册答案