
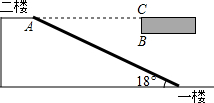
 如图,某大型商场在一楼至二楼之间安装有电梯,二楼地板厚BC为0.24米,AC=7米.
如图,某大型商场在一楼至二楼之间安装有电梯,二楼地板厚BC为0.24米,AC=7米.分析 (1)延长CB交电梯于点D,在Rt△ACD中,求出CD的长度,然后根据CB=0.24米,求出BD的长度,然后跟1.85米进行比较;
(2)过点B作BE⊥AD交AD于点E,在Rt△BDE中求出BE的长度即为限高.
解答 解:(1)延长CB将电梯于点D,
则△ACD为直角三角形,
∵AC=7米,∠CAD=18°,
∴CD=ACtan18°=7×0.31≈2,17(米),
∴BD=2.17-0.24=1.93>1.85,
故小明乘电梯没有碰头危险;
(2)过点B作BE⊥AD交AD于点E,
在Rt△BDE中,
∵BD=1.93米,∠EBD=18°,
∴BE=BDcos18°≈1.83(米).
∴货车上货物堆放的限高是1.83米.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据坡度构造直角三角形,利用三角函数的知识求解直角三角形,难度适中.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com