
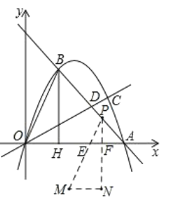
ЁОЬтФПЁПШчЭМЃЌжБЯпyЃНЉx+mгыХзЮяЯпyЃНax2+bxЖМОЙ§ЕуAЃЈ6ЃЌ0ЃЉЃЌЕуBЃЌЙ§BзїBHДЙжБxжсгкHЃЌOAЃН3OHЃЎжБЯпOCгыХзЮяЯпABЖЮНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕБЕуCЕФзнзјБъЪЧ![]() ЪБЃЌЧѓжБЯпOCгыжБЯпABЕФНЛЕуDЕФзјБъЃЛ
ЪБЃЌЧѓжБЯпOCгыжБЯпABЕФНЛЕуDЕФзјБъЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТНЋЁїOBHбиBAЗНЯђЦНвЦЕНЁїMPNЃЌЖЅЕуPЪМжедкЯпЖЮABЩЯЃЌЧѓЁїMPNгыЁїOACЙЋЙВВПЗжУцЛ§ЕФзюДѓжЕЃЎ
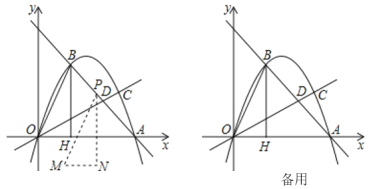
ЁОД№АИЁПЃЈ1ЃЉyЃН-![]() x2+3xЃЛЃЈ2ЃЉ(4ЃЌ2)ЃЛЃЈ3ЃЉ
x2+3xЃЛЃЈ2ЃЉ(4ЃЌ2)ЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЯШЧѓГіжБЯпABЕФНтЮіЪНЃЌЧѓГіЕуBзјБъЃЌдйНЋAЃЌBЕФзјБъДњШыyЃНax2+bxМДПЩЃЛ
ЃЈ2ЃЉЧѓГіжБЯпACЕФНтЮіЪНЃЌдйСЊСЂжБЯпOCгыжБЯпABЕФНтЮіЪНМДПЩЃЛ
ЃЈ3ЃЉЩшPMгыOCЁЂPAЗжБ№НЛгкGЁЂHЃЌPNгыOCЁЂOAЗжБ№НЛгкKЁЂFЃЌЗжБ№ЧѓГіжБЯпOBЃЌPMЃЌOCЕФНтЮіЪНЃЌдйЗжБ№гУКЌaЕФДњЪ§ЪНБэЪОГіHЃЌGЃЌEЃЌFЕФзјБъЃЌзюКѓЗжЧщПіЬжТлЃЌПЩЧѓГіЁїMPNгыЁїOACЙЋЙВВПЗжУцЛ§ЕФзюДѓжЕЃЎ
НтЃКЃЈ1ЃЉЁпжБЯпyЃНЉx+mЕуAЃЈ6ЃЌ0ЃЉЃЌ
ЁрЉ6+mЃН0ЃЌ
ЁрmЃН6ЃЌ
ЁрyABЃНЉx+6ЃЌ
ЁпOAЃН3OHЃЌ
ЁрOHЃН2ЃЌ
дкyABЃНЉx+6жаЃЌЕБxЃН2ЪБЃЌyЃН4ЃЌ
ЁрBЃЈ2ЃЌ4ЃЉЃЌ
НЋAЃЈ6ЃЌ0ЃЉЃЌBЃЈ2ЃЌ4ЃЉДњШыyЃНax2+bxЃЌ
ЕУЃЌ![]() ЃЌ
ЃЌ
НтЕУЃЌaЃНЉ![]() ЃЌbЃН3ЃЌ
ЃЌbЃН3ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊyЃН-![]() x2+3xЃЛ
x2+3xЃЛ
ЃЈ2ЃЉЁпжБЯпOCгыХзЮяЯпABЖЮНЛгкЕуCЃЌЧвЕуCЕФзнзјБъЪЧ![]() ЃЌ
ЃЌ
Ёр![]() ЃНЉ
ЃНЉ![]() x2+3xЃЌ
x2+3xЃЌ
НтЕУЃЌx1ЃН1ЃЈЩсШЅЃЉЃЌx2ЃН5ЃЌ
ЁрCЃЈ5ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЩшyOCЃНkxЃЌ
НЋCЃЈ5ЃЌ![]() ЃЉДњШыЃЌ
ЃЉДњШыЃЌ
ЕУЃЌkЃН![]() ЃЌ
ЃЌ
ЁрyOCЃН![]() xЃЌ
xЃЌ
СЊСЂ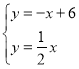 ЃЌ
ЃЌ
НтЕУЃЌxЃН4ЃЌyЃН2ЃЌ
ЁрЕуDЕФзјБъЮЊЃЈ4ЃЌ2ЃЉЃЛ
ЃЈ3ЃЉЩшжБЯпOBЕФНтЮіЪНЮЊyOBЃНmxЃЌЕуPзјБъЮЊЃЈaЃЌЉa+6ЃЉЃЌ
НЋЕуBЃЈ2ЃЌ4ЃЉДњШыЃЌ
ЕУЃЌmЃН2ЃЌ
ЁрyOBЃН2xЃЌ
гЩЦНвЦжЊЃЌPMЁЮOBЃЌ
ЁрЩшжБЯпPMЕФНтЮіЪНЮЊyPMЃН2x+nЃЌ
НЋPЃЈaЃЌЉa+6ЃЉДњШыЃЌ
ЕУЃЌЉa+6ЃН2a+nЃЌ
ЁрnЃН6Љ3aЃЌ
ЁрyPMЃН2x+6Љ3aЃЌ
ЩшPMгыOCЁЂPAЗжБ№НЛгкGЁЂHЃЌPNгыOCЁЂOAЗжБ№НЛгкKЁЂFЃЌ
СЊСЂ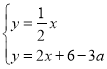 ЃЌ
ЃЌ
НтЕУЃЌxЃН2aЉ4ЃЌyЃНaЉ2ЃЌ
ЁрGЃЈ2aЉ4ЃЌaЉ2ЃЉЃЌyGЃНaЉ2ЃЌ
дкyPMЃН2x+6Љ3aжаЃЌ
ЕБyЃН0ЪБЃЌxЃН![]() ЃЌ
ЃЌ
ЁрEЃЈ![]() ЃЌ0ЃЉЃЌOEЃН
ЃЌ0ЃЉЃЌOEЃН![]() ЃЌ
ЃЌ
ЁпЕуPЕФКсзјБъЮЊaЃЌ
ЁрKЃЈaЃЌ![]() aЃЉЃЌFЃЈaЃЌ0ЃЉЃЌ
aЃЉЃЌFЃЈaЃЌ0ЃЉЃЌ
ЁрOFЃНaЃЌKFЃН![]() aЃЌ
aЃЌ
ЩшЁїMPNгыЁїOACЙЋЙВВПЗжУцЛ§ЮЊSЃЌ
ЂйЕБ0ЁмaЃМ4ЪБЃЌ
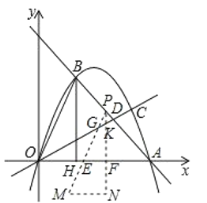
SЃНSЁїOFKЉSЁїOEGЃЌ
ЃН![]() ЁСaЁС
ЁСaЁС![]() aЉ
aЉ![]() ЃЈ
ЃЈ![]() ЃЉЃЈaЉ2ЃЉЃЌ
ЃЉЃЈaЉ2ЃЉЃЌ
ЃНЉ![]() a2+3aЉ3
a2+3aЉ3
ЃНЉ![]() ЃЈaЉ3ЃЉ2+
ЃЈaЉ3ЃЉ2+![]() ЃЌ
ЃЌ
ЁпЉ![]() ЃМ0ЃЌИљОнЖўДЮКЏЪ§ЕФЭМЯѓМАаджЪПЩжЊЃЌ
ЃМ0ЃЌИљОнЖўДЮКЏЪ§ЕФЭМЯѓМАаджЪПЩжЊЃЌ
ЁрЕБaЃН3ЪБSгазюДѓжЕ![]() ЃЛ
ЃЛ
ЂкЕБ4ЁмaЁм6ЪБЃЌ
SЃНSЁїPEF
ЃН![]() EFPF
EFPF
ЃН![]() ЃЈaЉ
ЃЈaЉ![]() a+3ЃЉЃЈЉa+6ЃЉ
a+3ЃЉЃЈЉa+6ЃЉ
ЃН![]()
ЃН![]() ЃЌ
ЃЌ
Ёп![]() ЃЌИљОнЖўДЮКЏЪ§ЕФЭМЯѓМАаджЪжЊЃЌЕБaЃН4ЪБЃЌSгазюДѓжЕ1ЃЛ
ЃЌИљОнЖўДЮКЏЪ§ЕФЭМЯѓМАаджЪжЊЃЌЕБaЃН4ЪБЃЌSгазюДѓжЕ1ЃЛ
Ёп![]()
ЁрЁїMPNгыЁїOACЙЋЙВВПЗжУцЛ§ЕФзюДѓжЕЮЊ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЦНЗж
ЦНЗж![]() .
.
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓжЄЃКЕу![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЛ
ЕФжаЕуЃЛ
ЃЈ3ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄ.
ЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
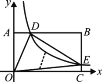
ЁОЬтФПЁПШчЭМЃЌдквдOЮЊдЕуЕФжБНЧзјБъЯЕжаЃЌОиаЮOABCЕФСНБпOCЁЂOAЗжБ№дкxжсЁЂyжсЕФе§АыжсЩЯЃЌЗДБШР§КЏЪ§![]() (xЃО0)гыABЯрНЛгкЕуDЃЌгыBCЯрНЛгкЕуEЃЌШєBD=3ADЃЌЧвЁїODEЕФУцЛ§ЪЧ9,дђkЕФжЕЪЧ( )
(xЃО0)гыABЯрНЛгкЕуDЃЌгыBCЯрНЛгкЕуEЃЌШєBD=3ADЃЌЧвЁїODEЕФУцЛ§ЪЧ9,дђkЕФжЕЪЧ( )
A.![]() B.
B.![]() C.
C.![]() D.12
D.12
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвдЯТИїЭМОљЪЧгЩБпГЄЮЊ1ЕФаЁе§ЗНаЮзщГЩЕФЭјИёЃЌЭМжаЕФЕуAЁЂBЁЂCЁЂDОљдкИёЕуЩЯЃЎ
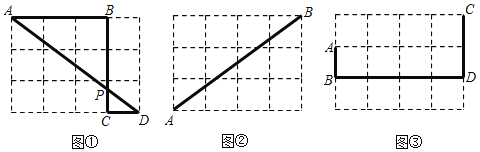
ЃЈ1ЃЉдкЭМЂйжаЃЌPCЃКPBЃНЁЁ ЃЎ
ЃЈ2ЃЉРћгУЭјИёКЭЮоПЬЖШЕФжБГпзїЭМЃЌБЃСєКлМЃЃЌВЛаДзїЗЈЃЎ
ЂйШчЭМЂкЃЌдкABЩЯеввЛЕуPЃЌЪЙAPЃН3ЃЎ
ЂкШчЭМЂлЃЌдкBDЩЯеввЛЕуPЃЌЪЙЁїAPBЁзЁїCPDЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯпyЃНax2+bx+cЃЈaЁй0ЃЉаЮзДШчЭМЃЌЯТСаНсТлЃКЂйbЃО0ЃЛЂкaЉb+cЃН0ЃЛЂлЕБxЃМЉ1ЛђxЃО3ЪБЃЌyЃО0ЃЛЂмвЛдЊЖўДЮЗНГЬax2+bx+c+1ЃН0ЃЈaЁй0ЃЉгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЎе§ШЗЕФгаЃЈЁЁЁЁЃЉ
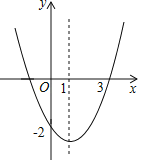
A.4ИіB.3ИіC.2ИіD.1Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєnЪЧвЛИіСНЮЛе§ећЪ§ЃЌЧвnЕФИіЮЛЪ§зжДѓгкЪЎЮЛЪ§зжЃЌдђГЦnЮЊЁАСНЮЛЕндіЪ§ЁБЃЈШч13ЃЌ35ЃЌ56ЕШЃЉЃЎдкФГДЮЪ§бЇШЄЮЖЛюЖЏжаЃЌУПЮЛВЮМгепашДггЩЪ§зж1ЃЌ2ЃЌ3ЃЌ4ЃЌ5ЃЌ6ЙЙГЩЕФЫљгаЕФЁАСНЮЛЕндіЪ§ЁБжаЫцЛњГщШЁ1ИіЪ§ЃЌЧвжЛФмГщШЁвЛДЮЃЎ
ЃЈ1ЃЉаДГіЫљгаИіЮЛЪ§зжЪЧ5ЕФЁАСНЮЛЕндіЪ§ЁБЃЛ
ЃЈ2ЃЉЧыгУСаБэЗЈЛђЪїзДЭМЃЌЧѓГщШЁЕФЁАСНЮЛЕндіЪ§ЁБЕФИіЮЛЪ§зжгыЪЎЮЛЪ§зжжЎЛ§ФмБЛ10ећГ§ЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПАйЛѕЩЬЕъЯњЪлФГжжБљЯфЃЌУПЬЈНјМл2500дЊЁЃЪаГЁЕїбаБэУїЃКЕБЯњЪлМлЮЊ2900дЊЪБЃЌЦНОљУПЬьФмЪлГі8ЬЈЃЛУПЬЈЪлМлУПНЕЕЭ10дЊЪБЃЌЦНОљУПЬьФмЖрЪлГі1ЬЈЁЃЃЈЯњЪлРћШѓ=ЯњЪлМлЁЊНјМлЃЉ
(1)ШчЙћЩшУПЬЈБљЯфНЕМлxдЊЃЌФЧУДУПЬЈБљЯфЕФЯњЪлРћШѓЮЊ дЊЃЌЦНОљУПЬьПЩЯњЪлБљЯф ЬЈЃЛЃЈгУКЌxЕФДњЪ§ЪНБэЪОЃЉ
(2)ЩЬЕъЯывЊЪЙетжжБљЯфЕФЯњЪлРћШѓЦНОљУПЬьДяЕН5600дЊЃЌЧвОЁПЩФмЕиЧхПеБљЯфПтДцЃЌУПЬЈБљЯфЕФЖЈМлгІЮЊЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
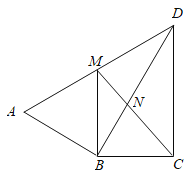
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCжаЃЌЁЯC=90ЁуЃЌAC=BC= ![]() ЃЌНЋЁїABCШЦЕуAЫГЪБеыЗНЯђа§зЊ60ЁуЕНЁїABЁфCЁфЕФЮЛжУЃЌСЌНгCЁфBЃЎ
ЃЌНЋЁїABCШЦЕуAЫГЪБеыЗНЯђа§зЊ60ЁуЕНЁїABЁфCЁфЕФЮЛжУЃЌСЌНгCЁфBЃЎ
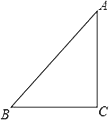
ЃЈ1ЃЉЧыФудкЭМжаАбЭМВЙЛЭъећЃЛ
ЃЈ2ЃЉЧѓCЁфBЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЖўДЮКЏЪ§y=|a|x2+bx+cЕФЭМЯѓОЙ§A(m,n)ЁЂB(0,y1)ЁЂC(3Ѓm,n)ЁЂD(![]() , y2)ЁЂE(2,y3)ЃЌдђy1ЁЂy2ЁЂy3ЕФДѓаЁЙиЯЕЪЧ( ).
, y2)ЁЂE(2,y3)ЃЌдђy1ЁЂy2ЁЂy3ЕФДѓаЁЙиЯЕЪЧ( ).
A. y1< y2< y3B. y1 < y3< y2C. y3< y2< y1D. y2< y3< y1
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com