
【题目】求两个正整数的最大公约数是常见的数学问题,中国古代数学专著《九章算术》中便记载了求两个正整数最大公约数的一种方法﹣﹣更相减损术,术曰:“可半者半之,不可半者,副置分母、子之数,以少成多,更相减损,求其等也.以等数约之”,意思是说,要求两个正整数的最大公约数,先用较大的数减去较小的数,得到差,然后用减数与差中的较大数减去较小数,以此类推,当减数与差相等时,此时的差(或减数)即为这两个正整数的最大公约数.
例如:求91与56的最大公约数
解:
请用以上方法解决下列问题:
(1)求108与45的最大公约数;
(2)求三个数78、104、143的最大公约数.

【答案】(1)9;(2)13.
【解析】
试题分析:(1)根据题目,首先弄懂题意,然后根据例子写出答案即可;
(2)可以先求出104与78的最大公约数为 26,再利用辗转相除法,我们可以求出26 与 143的最大公约数为13,进而得到答案.
试题解析:(1)108﹣45=63,63﹣45=18,27﹣18=9,18﹣9=9,所以108与45的最大公约数是9;
(2)先求104与78的最大公约数,104﹣78=26,78﹣26=52,52﹣26=26,所以104与78的最大公约数是26;
再求26与143的最大公约数,143﹣26=117,117﹣26=91,91﹣26=65,65﹣26=39,39﹣26=13,26﹣13=13,所以,26与143的最大公约数是13,∴78、104、143的最大公约数是13.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线DE交AC于D,交AB于E,∠DBC=15°,则∠A的度数是( ) 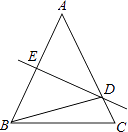
A.50°
B.20°
C.30°
D.25°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于点F. 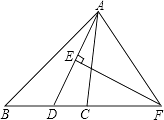
(1)求证:∠FAD=∠FDA;
(2)若∠B=50°,求∠CAF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,下列各组角的位置,判断错误的是( ) 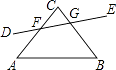
A.∠C和∠CFG是同旁内角
B.∠CGF和∠AFG是内错角
C.∠BGF和∠A是同旁内角
D.∠BGF和∠AFD是同位角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解.并规定:F(n)=![]() .例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所有3×4是12的最佳分解,所以F(12)=
.例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所有3×4是12的最佳分解,所以F(12)=![]() .
.
(1)如果一个正整数a是另外一个正整数b的平方,我们称正整数a是完全平方数.求证:对任意一个完全平方数m,总有F(m)=1;
(2)如果一个两位正整数t,t=10x+y(1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们称这个数t为“吉祥数”,求所有“吉祥数”中F(t)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一列按一定顺序和规律排列的数:
第一个数是![]() ;
;
第二个数是![]() ;
;
第三个数是![]() ;
;
…
对任何正整数n,第n个数与第(n+1)个数的和等于![]() .
.
(1)经过探究,我们发现:![]() ,
,![]() ,
,![]() ;
;
设这列数的第5个数为a,那么![]() ,
,![]() ,
,![]() ,哪个正确?
,哪个正确?
请你直接写出正确的结论;
(2)请你观察第1个数、第2个数、第3个数,猜想这列数的第n个数(即用正整数n表示第n数),并且证明你的猜想满足“第n个数与第(n+1)个数的和等于![]() ”;
”;
(3)设M表示![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,这2016个数的和,即
,这2016个数的和,即![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在矩形ABCD中,AB= ![]() AD,点E、F分别在AB、AD上且不与顶点A、B、D重合,
AD,点E、F分别在AB、AD上且不与顶点A、B、D重合, ![]() , 圆O过A、E、F三点。
, 圆O过A、E、F三点。
(1)求证:圆O与CE相切于点E.
(2)如图1,若AF=2FD,且![]() ,求
,求![]() 的值。
的值。
(3)如图2,若EF=EC,且圆O与边CD相切,求![]() 的值。
的值。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)2﹣(﹣18)+(﹣7)﹣15
(2)(﹣48)÷8﹣(﹣25)×(﹣6)
(3)﹣14﹣|2﹣5|+6×(﹣ ![]() )
)
(4)﹣36×( ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() )÷(﹣2)
)÷(﹣2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com