
【题目】如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于点F. 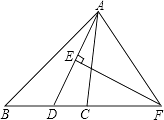
(1)求证:∠FAD=∠FDA;
(2)若∠B=50°,求∠CAF的度数.
【答案】
(1)解:∵AD的垂直平分线交BC的延长线于点F,
∴AF=DF,
∴∠FAD=∠FDA
(2)解:∵∠FAD=∠FAC+∠CAD,∠FDA=∠B+∠BAD,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠FAC=∠B=50°.
故答案为:50°
【解析】(1)根据线段垂直平分线得出AF=DF,根据等腰三角形的性质推出∠FAD=∠FDA,(2)根据角平分线得出∠BAD=∠CAD,根据三角形外角性质推出即可.
【考点精析】解答此题的关键在于理解线段垂直平分线的性质的相关知识,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中任意一点P(x0 , y0),经平移后对应点为P1(x0+3,y0﹣3),将△ABC作同样平移得到△DEF. 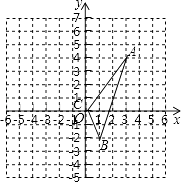
(1)求△ABC的面积;
(2)请写出D,E,F的坐标,并在图中画出△DEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高中自主招生考试只考数学和物理,数学与物理成绩按7:3计入综合成绩.已知小明数学成绩为95分,综合成绩为92分,那么小明的物理成绩为_____分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ABC=90°,D是直线AB上的点,AD=BC.过点A作AF⊥AB,并截取AF=BD,连接DC,DF,CF. 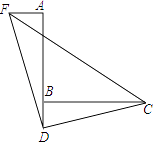
(1)判断△CDF的形状并证明.
(2)若BC=6,AF=2,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求两个正整数的最大公约数是常见的数学问题,中国古代数学专著《九章算术》中便记载了求两个正整数最大公约数的一种方法﹣﹣更相减损术,术曰:“可半者半之,不可半者,副置分母、子之数,以少成多,更相减损,求其等也.以等数约之”,意思是说,要求两个正整数的最大公约数,先用较大的数减去较小的数,得到差,然后用减数与差中的较大数减去较小数,以此类推,当减数与差相等时,此时的差(或减数)即为这两个正整数的最大公约数.
例如:求91与56的最大公约数
解:
请用以上方法解决下列问题:
(1)求108与45的最大公约数;
(2)求三个数78、104、143的最大公约数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,池塘边有一块长为20米,宽为12米的长方形土地,现在将其余三面留出宽都是x米的小路,中间余下的长方形部分做菜地,用代数式表示: 
(1)菜地的长a=米,宽b=米;
(2)菜地的面积S=平方米;
(3)求当x=2米时,菜地的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com