
【题目】如图,已知直线y=﹣ ![]() x+3分别交x轴、y轴于点A、B,P是抛物线y=﹣
x+3分别交x轴、y轴于点A、B,P是抛物线y=﹣ ![]() x2+2x+5的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=﹣
x2+2x+5的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=﹣ ![]() x+3于点Q,则当PQ=BQ时,a的值是 .
x+3于点Q,则当PQ=BQ时,a的值是 . 
【答案】﹣1,4,4+2 ![]() ,4﹣2
,4﹣2 ![]()
【解析】解:设点P的坐标为(a,﹣ ![]() a2+2a+5),
a2+2a+5),
则点Q为(a,﹣ ![]() a+3),点B为(0,3),
a+3),点B为(0,3),
①当点P在点Q上方时,BQ= ![]() =|
=| ![]() a|,
a|,
PQ=﹣ ![]() a2+2a+5﹣(﹣
a2+2a+5﹣(﹣ ![]() a+3)=﹣
a+3)=﹣ ![]() a2+
a2+ ![]() a+2,
a+2,
∵PQ=BQ,
当a>0时,
∴ ![]() a=﹣
a=﹣ ![]() a2+
a2+ ![]() a+2,
a+2,
整理得:a2﹣3a﹣4=0,
解得:a=﹣1(舍去)或a=4,
当a<0时,则﹣ ![]() a=﹣
a=﹣ ![]() a2+
a2+ ![]() a+2,
a+2,
解得:a=4+2 ![]() (舍去)或a=4﹣2
(舍去)或a=4﹣2 ![]() ;
;
②当点P在点Q下方时,BQ= ![]() =|
=| ![]() a|,
a|,
PQ=﹣ ![]() a+3﹣(﹣
a+3﹣(﹣ ![]() a2+2a+5)=
a2+2a+5)= ![]() a2﹣
a2﹣ ![]() a﹣2,
a﹣2,
由题意得,PQ=BQ,
当a>0时,
则 ![]() a=
a= ![]() a2﹣
a2﹣ ![]() a﹣2,
a﹣2,
整理得:a2﹣8a﹣4=0,
解得:a=4+2 ![]() 或a=4﹣2
或a=4﹣2 ![]() (舍去).
(舍去).
当a<0时,则﹣ ![]() a=
a= ![]() a2﹣
a2﹣ ![]() a﹣2,
a﹣2,
解得:a=﹣1或a=4(舍去),
综上所述,a的值为:﹣1,4,4+2 ![]() ,4﹣2
,4﹣2 ![]() .
.
所以答案是:﹣1,4,4+2 ![]() ,4﹣2
,4﹣2 ![]() .
.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】定义:两条抛物线顶点都在直线y=x上,且两条抛物线关于原点成中心对称,则称这两条抛物线为一对“友好抛物线”.

(1)抛物线y=2(x-1)2+1如图1所示,请画出它的“友好抛物线”,并直接写出它的解析式;
(确认无误后,请用黑色水笔描黑)
(2)一对“友好抛物线”,其中一条抛物线的解析式为y= -(x+h)2-h,这对“友好抛物线”与y轴交点记为A,B,记AB=n(当A与B重合时,记n=0),现我们来探究n与h的关系;
①当h≥0时,如图2所示,求n与h的函数关系式;
②当h<0时,求n与h的函数关系式;
(3)在(2)的条件下,要使 ![]() ≤n≤
≤n≤ ![]() ,试直接写出h的取值范围.
,试直接写出h的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y= ![]() 和y=﹣
和y=﹣ ![]() 的图象分别是l1和l2 . 设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则△PAB的面积为 .
的图象分别是l1和l2 . 设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则△PAB的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市每天能出售甲、乙两种肉集装箱共21箱,且甲集装箱3天的销售量与乙集装箱4天的销售量相同.
(1)求甲、乙两种肉类集装箱每天分别能出售多少箱?
(2)若甲种肉类集装箱的进价为每箱200元,乙种肉类集装箱的进价为每箱180元,现超市打算购买甲、乙两种肉类集装箱共100箱,且手头资金不到18080元,则该超市有几种购买方案?
(3)若甲种肉类集装箱的售价为每箱260元,乙种肉类集装箱的售价为每箱230元,在(2)的情况下,哪种方案获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在多边形ABCDE中,∠A=∠AED=∠D=90°,AB=5,AE=2,ED=3,过点E作EF∥CB交AB于点F,FB=1,过AE上的点P作PQ∥AB交线段EF于点O,交折线BCD于点Q,设AP=x,POOQ=y.
(1)①延长BC交ED于点M,则MD= , DC=;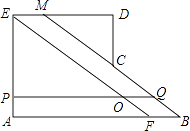
(2)求y关于x的函数解析式;
(3)当a≤x≤ ![]() (a>0)时,9a≤y≤6b,求a,b的值;
(a>0)时,9a≤y≤6b,求a,b的值;
(4)当1≤y≤3时,请直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=5,AC=9,S△ABC= ![]() ,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.
,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.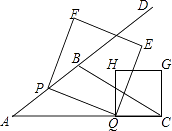
(1)求tanA的值;
(2)设点P运动时间为t,正方形PQEF的面积为S,请探究S是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由;
(3)当t为何值时,正方形PQEF的某个顶点(Q点除外)落在正方形QCGH的边上,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,O为BC的中点,AB与⊙O相切于点D. 
(1)求证:AC是⊙O的切线;
(2)若∠B=33°,⊙O的半径为1,求BD的长.(结果精确到0.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】神仙居景区门票价格80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包 括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用y1(元)及节假日门票费用y2(元)与游客x(人)之间的函数关系如图所示.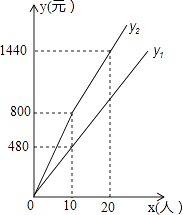
(1)a= , b=;
(2)直接写出y1、y2与x之间的函数关系式;
(3)导游小王6月10日(非节假日)带A旅游团,6月20日(端午节)带B旅游团到神仙居景区旅游,两团共计50人,两次共付门票费用3040元,求A、B两个旅游团各多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点C(1,0),直线y=﹣x+7与两坐标轴分别交于A、B两点,D、E分别是AB,OA上的动点,当△CDE周长最小时,点D坐标为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com