
【题目】如图,在△ABC中,AB=5,AC=9,S△ABC= ![]() ,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.
,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.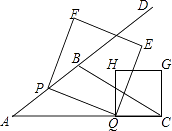
(1)求tanA的值;
(2)设点P运动时间为t,正方形PQEF的面积为S,请探究S是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由;
(3)当t为何值时,正方形PQEF的某个顶点(Q点除外)落在正方形QCGH的边上,请直接写出t的值.
【答案】
(1)
解:如图1,过点B作BM⊥AC于点M,

∵AC=9,S△ABC= ![]() ,
,
∴ ![]() ACBM=
ACBM= ![]() ,即
,即 ![]() ×9BM=
×9BM= ![]() ,
,
解得BM=3.
由勾股定理,得
AM= ![]() =
= ![]() =4,
=4,
则tanA= ![]() =
= ![]()
(2)
解:存在.
如图2,

过点P作PN⊥AC于点N.
依题意得AP=CQ=5t.
∵tanA= ![]() ,
,
∴AN=4t,PN=3t.
∴QN=AC﹣AN﹣CQ=9﹣9t.
根据勾股定理得到:PN2+NQ2=PQ2,
S正方形PQEF=PQ2=(3t)2+(9﹣9t)2=90t2﹣162t+81(0<t< ![]() ).
).
∵﹣ ![]() =
= ![]() =
= ![]() 在t的取值范围之内,
在t的取值范围之内,
∴S最小值= ![]() =
= ![]() =
= ![]()
(3)
解: 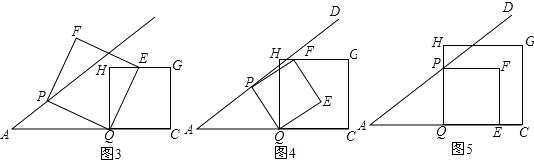

①如图3,当点E在边HG上时,t1= ![]() ;
;
②如图4,当点F在边HG上时,t2= ![]() ;
;
③如图5,当点P边QH(或点E在QC上)时,t3=1
④如图6,当点F边CG上时,t4= ![]()
【解析】(1)如图1,过点B作BM⊥AC于点M,利用面积法求得BM的长度,利用勾股定理得到AM的长度,最后由锐角三角函数的定义进行解答;(2)如图2,过点P作PN⊥AC于点N.利用(1)中的结论和勾股定理得到PN2+NQ2=PQ2 , 所以由正方形的面积公式得到S关于t的二次函数,利用二次函数的顶点坐标公式和二次函数图象的性质来求其最值;(3)需要分类讨论:当点E在边HG上、点F在边HG上、点P边QH(或点E在QC上)、点F边C上时相对应的t的值.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD=CD=8,AB=CB=6,点E,F,G,H分别是DA,AB,BC,CD的中点. 
(1)求证:四边形EFGH是矩形;
(2)若DA⊥AB,求四边形EFGH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网络购物发展十分迅速,某企业有4000名职工,从中随机抽取350人,按年龄分布和对网上购物所持态度情况进行了调查,并将调查结果绘成了条形图1和扇形图2. 
(1)这次调查中,如果职工年龄的中位数是整数,那么这个中位数所在的年龄段是哪一段?
(2)如果把对网络购物所持态度中的“经常(购物)”和“偶尔(购物)”统称为“参与购物”,那么这次接受调查的职工中“参与网购”的人数是多少?
(3)这次调查中,“25﹣35”岁年龄段的职工“从不(网购)”的有22人,它占“25﹣35”岁年龄段接受调查人数的百分之几?
(4)请估计该企业“从不(网购)”的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1中的摩天轮可抽象成一个圆,圆上一点离地面的高度y(m)与旋转时间x(min)之间的关系如图2所示. 
(1)根据图2填表:
x(min) | 0 | 3 | 6 | 8 | 12 | … |
y(m) | … |
(2)变量y是x的函数吗?为什么?
(3)根据图中的信息,请写出摩天轮的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣ ![]() x+3分别交x轴、y轴于点A、B,P是抛物线y=﹣
x+3分别交x轴、y轴于点A、B,P是抛物线y=﹣ ![]() x2+2x+5的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=﹣
x2+2x+5的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=﹣ ![]() x+3于点Q,则当PQ=BQ时,a的值是 .
x+3于点Q,则当PQ=BQ时,a的值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣ ![]() x2+mx+n与x轴交于A (﹣2,0)、B两点,与y轴交于点C.抛物线对称轴为直线x=3,且对称轴与x轴交于点D.
x2+mx+n与x轴交于A (﹣2,0)、B两点,与y轴交于点C.抛物线对称轴为直线x=3,且对称轴与x轴交于点D.
(1)求抛物线的解析式;
(2)点P在线段BC上从点C开始向点B运动(点P不与点B、C重合),速度为每秒 ![]() 个单位,设运动时间为t(单位:s),过点P作x轴的垂线与抛物线相交于点F.求四边形CDBF的面积S关于t的函数关系式.
个单位,设运动时间为t(单位:s),过点P作x轴的垂线与抛物线相交于点F.求四边形CDBF的面积S关于t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△AOB∽△DOC,∠AOB=∠COD=90°,M为OA的中点,OA=6,OB=8,将△COD绕O点旋转,连接AD,CB交于P点,连接MP,则MP的最大值( )
A.7
B.8
C.9
D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市民营经济持续发展,2015年城镇民营企业就业人数突破20万.为了解城镇民营企业员工每月的收入状况,统计局对全市城镇民营企业员工2015年月平均收入随机抽样调查,将抽样的数据按“2000元以内”、“2000元~4000元”、“4000元~6000元”和“6000元以上”分为四组,进行整理,分别用A,B,C,D表示,得到下列两幅不完整的统计图.
由图中所给出的信息解答下列问题:
(1)本次抽样调查的员工有人,在扇形统计图中x的值为 , 表示“月平均收入在2000元以内”的部分所对应扇形的圆心角的度数是;
(2)将不完整的条形图补充完整,并估计我市2015年城镇民营企业20万员工中,每月的收入在“2000元~4000元”的约多少人?
(3)统计局根据抽样数据计算得到,2016年我市城镇民营企业员工月平均收入为4872元,请你结合上述统计的数据,谈一谈用平均数反映月收入情况是否合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△BCD中,AB=DC,AC=DB,AC、DB交于点M. 
(1)求证:△ABC≌△DCB;
(2)作CN∥BD,BN∥AC,CN交BN于点N,求证:四边形BNCM是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com