
【题目】如图,在△ABC和△BCD中,AB=DC,AC=DB,AC、DB交于点M. 
(1)求证:△ABC≌△DCB;
(2)作CN∥BD,BN∥AC,CN交BN于点N,求证:四边形BNCM是菱形.
【答案】
(1)证明:∵在△ABC和△DCB中,
 .
.
∴△ABC≌△DCB(SSS);

(2)∵△ABC≌△DCB,
∴∠DBC=∠ACB,
∴MB=MC.
∵CN∥BD,BN∥AC,
∴四边形BNCM为平行四边形.
又∵MB=MC,
∴平行四边形BNCM为菱形.
【解析】(1)由全等三角形的判定定理SSS证得结论;(2)首先根据△ABC≌△DCB可得∠DBC=∠ACB,进而可得BM=CM,根据CN∥BD、BN∥AC,可判定四边形BNCM是平行四边形,再根据邻边相等的平行四边形是菱形可得结论.
【考点精析】通过灵活运用菱形的判定方法,掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=5,AC=9,S△ABC= ![]() ,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.
,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.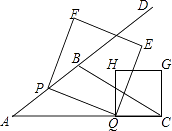
(1)求tanA的值;
(2)设点P运动时间为t,正方形PQEF的面积为S,请探究S是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由;
(3)当t为何值时,正方形PQEF的某个顶点(Q点除外)落在正方形QCGH的边上,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A、B的坐标分别为(0,3)、(7,0),点C在第一象限,AC∥x轴,∠OBC=45°.
(1)求点C的坐标;
(2)点D在线段AC上,CD=1,点E的坐标为(n,0),在直线DE的右侧作∠DEG=45°,直线EG与直线BC相交于点F,设BF=m,当n<7且n≠0时,求m关于n的函数解析式,并直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图从一个建筑物的A处测得对面楼BC的顶部B的仰角为37°,底部C的俯角为45°,观察点与楼的水平距离AD为40m,求楼BC的高度(参考数据:sin37°≈0.60;cos37°≈0.80;tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点C(1,0),直线y=﹣x+7与两坐标轴分别交于A、B两点,D、E分别是AB,OA上的动点,当△CDE周长最小时,点D坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB. 
(1)判断直线BD和⊙O的位置关系,并给出证明;
(2)当tan∠AEC= ![]() ,BC=8时,求OD的长.
,BC=8时,求OD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组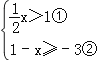 请结合题意,完成本题解答.
请结合题意,完成本题解答.
(1)解不等式①,得 ;
(2)解不等式②,得 ;
(3)把不等式①和②的解集在数轴上表示出来:![]() ;
;
(4)原不等式组的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,交BC于点E(BE>EC),且BD=2![]() .过点D作DF∥BC,交AB的延长线于点F.
.过点D作DF∥BC,交AB的延长线于点F.
(1)求证:DF为⊙O的切线;
(2)若∠BAC=60°,DE=![]() ,求图中阴影部分的面积;
,求图中阴影部分的面积;
(3)若![]() =
=![]() ,DF+BF=8,如图2,求BF的长.
,DF+BF=8,如图2,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,延长BC至M,使BM=DN,连接MN交BD延长线于点E.
(1)求证:BD+2DE=![]() BM.
BM.
(2)如图2,连接BN交AD于点F,连接MF交BD于点G.若AF:FD=1:2,且CM=2,则线段DG=_____;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com