
【题目】如图,在四边形ABCD中,AD=CD=8,AB=CB=6,点E,F,G,H分别是DA,AB,BC,CD的中点. 
(1)求证:四边形EFGH是矩形;
(2)若DA⊥AB,求四边形EFGH的面积.
【答案】
(1)解:

连接AC、BD,交于点O,如图.
∵点E、F、G、H分别是DA、AB、BC、CD的中点,
∴EF∥BD∥GH,EH∥AC∥FG,
EF=GH= ![]() BD,EH=FG=
BD,EH=FG= ![]() AC,
AC,
∴四边形EFGH是矩形.
∵AD=CD,AB=CB,
∴点D、B都在线段AC的垂直平分线上,
∴DB垂直平分AC,
∴DB⊥AC,OA=OC.
∵EF∥DB,
∴EF⊥AC.
∵FG∥AC,
∴EF⊥FG,
∴EFGH是矩形
(2)解:∵DA⊥AB,AD=8,AB=6,
∴DB=10.
∴EF= ![]() BD=5.
BD=5.
∵S△BAD= ![]() ABAD=
ABAD= ![]() BDAO,
BDAO,
∴AO= ![]() =
= ![]() =
= ![]() ,
,
∴OC= ![]() ,AC=
,AC= ![]() ,
,
∴FG= ![]() AC=
AC= ![]() ,
,
∴S矩形EFGH=FGEF= ![]() ×5=24.
×5=24.
【解析】(1)连接AC、BD,交于点O,运用三角形中位线定理可证到四边形EFGH是平行四边形,要证四边形EFGH是矩形,只需证EF⊥FG,由于EF∥BD,FG∥AC,只需证DB⊥AC,只需运用线段垂直平分线性质定理的逆定理就可解决问题;(2)要求矩形EFGH的面积,只需求出EF、FG的值,只需求出BD、AC,运用勾股定理就可求出BD,运用面积法就可求出AO,从而求出AC,问题得以解决.
【考点精析】本题主要考查了矩形的判定方法的相关知识点,需要掌握有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形才能正确解答此题.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=3时,这两个二次函数的最大值之和等于( ) 
A.![]()
B.![]()
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家环保局统一规定,空气质量分为5级:1级质量为优;2级质量为良;3级质量为轻度污染;4级质量为中度污染;5级质量为重度污染.某城市随机抽取了一年中某些天的空气质量检测结果,并整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列各题: 
(1)本次调查共抽取了天的空气质量检测结果进行统计;
(2)补全条形统计图;
(3)扇形统计图中3级空气质量所对应的圆心角为°;
(4)如果空气污染达到中度污染或者以上,将不适宜进行户外活动,根据目前的统计,请你估计该年该城市只有多少天适宜户外活动.(一年天数按365天计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:两条抛物线顶点都在直线y=x上,且两条抛物线关于原点成中心对称,则称这两条抛物线为一对“友好抛物线”.

(1)抛物线y=2(x-1)2+1如图1所示,请画出它的“友好抛物线”,并直接写出它的解析式;
(确认无误后,请用黑色水笔描黑)
(2)一对“友好抛物线”,其中一条抛物线的解析式为y= -(x+h)2-h,这对“友好抛物线”与y轴交点记为A,B,记AB=n(当A与B重合时,记n=0),现我们来探究n与h的关系;
①当h≥0时,如图2所示,求n与h的函数关系式;
②当h<0时,求n与h的函数关系式;
(3)在(2)的条件下,要使 ![]() ≤n≤
≤n≤ ![]() ,试直接写出h的取值范围.
,试直接写出h的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小山岗的斜坡AC的坡角α=45°,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,小山岗的高AB约为(结果取整数,参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50)( ) 
A.164m
B.178m
C.200m
D.1618m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=kx2+ ![]() x+
x+ ![]() (k是常数).
(k是常数).
(1)若该函数的图象与x轴有两个不同的交点,试求k的取值范围;
(2)若点(1,k)在某反比例函数图象上,要使该反比例函数和二次函数y=kx2+ ![]() x+
x+ ![]() 都是y随x的增大而增大,求k应满足的条件及x的取值范围;
都是y随x的增大而增大,求k应满足的条件及x的取值范围;
(3)若抛物线y=kx2+ ![]() x+
x+ ![]() 与x轴交于A(xA , 0)、B(xB , 0)两点,且xA<xB , xA2+xB2=34,若与y轴不平行的直线y=ax+b经过点P(1,3),且与抛物线交于Q1(x1 , y1)、Q2(x2 , y2)两点,试探究
与x轴交于A(xA , 0)、B(xB , 0)两点,且xA<xB , xA2+xB2=34,若与y轴不平行的直线y=ax+b经过点P(1,3),且与抛物线交于Q1(x1 , y1)、Q2(x2 , y2)两点,试探究 ![]() 是否为定值,并写出探究过程.
是否为定值,并写出探究过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农庄计划在30亩空地上全部种植蔬菜和水果,菜农小张和果农小李分别承包了种植蔬菜和水果的任务.小张种植每亩蔬菜的工资y(元)与种植面积m(亩)之间的函数如图①所示,小李种植水果所得报酬z(元)与种植面积n(亩)之间函数关系如图②所示. 
(1)如果种植蔬菜20亩,则小张种植每亩蔬菜的工资是元,小张应得的工资总额是元,此时,小李种植水果亩,小李应得的报酬是元;
(2)当10<n≤30时,求z与n之间的函数关系式;
(3)设农庄支付给小张和小李的总费用为w(元),当10<m≤30时,求w与m之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=5,AC=9,S△ABC= ![]() ,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.
,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.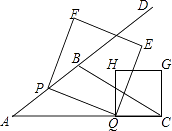
(1)求tanA的值;
(2)设点P运动时间为t,正方形PQEF的面积为S,请探究S是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由;
(3)当t为何值时,正方形PQEF的某个顶点(Q点除外)落在正方形QCGH的边上,请直接写出t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com