
【题目】当x=m或x=n(m≠n)时,代数式x2-2x的值相等,则当x=m+n时,代数式x2-2x的值为 .
【答案】0
【解析】解:∵当x=m或x=n(m≠n)时,代数式x2-2x的值相等,
∴m2-2m=n2-2n,
即:m2-n2=2m-2n,
左右两边分别分解因式得:
(m+n)(m-n)=2(m-n),
∵m≠n,即m-n![]() 0,左右两边同时除以m-n,
0,左右两边同时除以m-n,
∴m+n=2.
当x=m+n时,原式=(m+n)2-2(m+n)=22-2![]() 2=4-4=0.
2=4-4=0.
所以答案是:0.
【考点精析】通过灵活运用代数式求值和因式分解的应用,掌握求代数式的值,一般是先将代数式化简,然后再将字母的取值代入;求代数式的值,有时求不出其字母的值,需要利用技巧,“整体”代入;因式分解是整式乘法的逆向变形,可以应用与数字计算、求值、整除性问题、判断三角形的形状、解方程即可以解答此题.


科目:初中数学 来源: 题型:
【题目】学了统计知识后,小刚就本班同学上学“喜欢的出行方式”进行了一次调查.图(1)和图(2)是他根据采集的数据绘制的两幅不完整的统计图,请根据图中提供的信息解答以下问题: 
(1)补全条形统计图,并计算出“骑车”部分所对应的圆心角的度数;
(2)如果全年级共600名同学,请估算全年级步行上学的学生人数;
(3)若由3名“喜欢乘车”的学生,1名“喜欢步行”的学生,1名“喜欢骑车”的学生组队参加一项活动,欲从中选出2人担任组长(不分正副),列出所有可能的情况,并求出2人都是“喜欢乘车”的学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杰瑞公司成立之初投资1500万元购买新生产线生产新产品,此外,生产每件该产品还需要成本60元.按规定,该产品售价不得低于100元/件且不得超过180元/件,该产品销售量y(万件)与产品售价x(元)之间的函数关系如图所示. 
(1)求y与x之间的函数关系式,并写出x的取值范围;
(2)第一年公司是盈利还是亏损?求出当盈利最大或者亏损最小时的产品售价;
(3)在(2)的前提下,即在第一年盈利最大或者亏损最小时,第二年公司重新确定产品售价,能否使两年共盈利达1340万元?若能,求出第二年产品售价;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在边长为8的等边△ABC中,CD⊥AB,垂足为D,⊙O的圆心与点D重合,⊙O与线段CD交于点E,若将⊙O沿DC方向向上平移1cm后,如图②,⊙O恰与△ABC的边AC,BC相切,则图①中CE的长为cm. 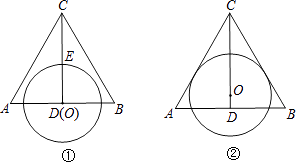
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F. 
(1)求证:EF⊥AB;
(2)若∠C=30°,EF= ![]() ,求EB的长.
,求EB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等边三角形.
(1)动手操作:如图1,点D在△ABC内,且∠BDC=150°,CD=1,BD=![]() , 把△BCD绕着点C顺时针旋转,使点B旋转到点A,得到△AEC.
, 把△BCD绕着点C顺时针旋转,使点B旋转到点A,得到△AEC.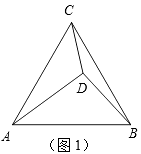
①依题意补全图1;(确认无误后,请用黑色水笔描黑)
②连接DE,则线段DE= , AD=;
(2)应用拓展:如图2,点D在△ABC外,且CD=3,BD=4,AD=5,求∠BDC的度数.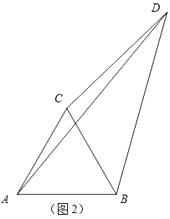
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD=CD=8,AB=CB=6,点E,F,G,H分别是DA,AB,BC,CD的中点. 
(1)求证:四边形EFGH是矩形;
(2)若DA⊥AB,求四边形EFGH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1中的摩天轮可抽象成一个圆,圆上一点离地面的高度y(m)与旋转时间x(min)之间的关系如图2所示. 
(1)根据图2填表:
x(min) | 0 | 3 | 6 | 8 | 12 | … |
y(m) | … |
(2)变量y是x的函数吗?为什么?
(3)根据图中的信息,请写出摩天轮的直径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com