
【题目】已知△ABC是等边三角形.
(1)动手操作:如图1,点D在△ABC内,且∠BDC=150°,CD=1,BD=![]() , 把△BCD绕着点C顺时针旋转,使点B旋转到点A,得到△AEC.
, 把△BCD绕着点C顺时针旋转,使点B旋转到点A,得到△AEC.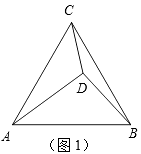
①依题意补全图1;(确认无误后,请用黑色水笔描黑)
②连接DE,则线段DE= , AD=;
(2)应用拓展:如图2,点D在△ABC外,且CD=3,BD=4,AD=5,求∠BDC的度数.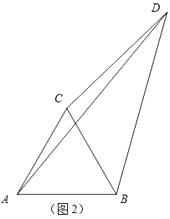
【答案】
(1)解:补全图形如下图: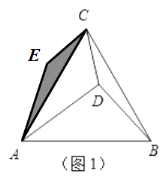 ;1;
;1;![]()
(2)
解:把△BCD绕着点C顺时针旋转,使点B旋转到点A,得到△ACF,连接DF.
∴∠DCF=∠BCA=60°,CF=CD=3,AF=BD=4
∴△CDF是等边三角形,∴DF=CD=3,∠CFD=60°
∵AD2=52=25,AF2+DF2=42+32=25
∴AD2= AF2+DF2,∴∠AFD=90°
∴∠AFC=∠AFD-∠CFD=90°-60°=30°
∴∠BDC=∠AFC=30° .
答:∠BDC的度数是30° .
【解析】本题在作旋转图形时,注意找准旋转中心、旋转方向、旋转角度三要素. 第2题利用旋转的性质和线段之间的关系,通过勾股定理的逆定理求解即可.
【考点精析】关于本题考查的等边三角形的性质和勾股定理的逆定理,需要了解等边三角形的三个角都相等并且每个角都是60°;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形才能得出正确答案.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD. 
(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小红、小兵玩捉迷藏游戏,小红、小兵可以在A,B,C三个地点中任意一处藏身,小明去寻找他们.
(1)求小明在B处找到小红的概率;
(2)求小明在同一地点找到小红和小兵的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小山岗的斜坡AC的坡角α=45°,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,小山岗的高AB约为(结果取整数,参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50)( ) 
A.164m
B.178m
C.200m
D.1618m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的棱长为1的正方体中,A,B,C,D,E是正方体的顶点,M是棱CD的中点.动点P从点D出发,沿着D→A→B的路线在正方体的棱上运动,运动到点B停止运动.设点P运动的路程是x,y=PM+PE,则y关于x的函数图象大致为( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,AB=BC,以AB为直径的圆交AC于点D,过点D的⊙O的切线交BC于点E.若CD=5,CE=4,则⊙O的半径是( ) 
A.3
B.4
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com