
【题目】如图,AB是⊙O的直径,AC是上半圆的弦,过点C作⊙O的切线DE交AB的延长线于点E,过点A作切线DE的垂线,垂足为D,且与⊙O交于点F,设∠DAC,∠CEA的度数分别是α,β. 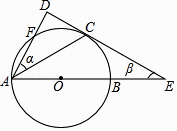
(1)用含α的代数式表示β,并直接写出α的取值范围;
(2)连接OF与AC交于点O′,当点O′是AC的中点时,求α,β的值.
【答案】
(1)解:)连接OC.
∵DE是⊙O的切线,
∴OC⊥DE,
∵AD⊥DE,
∴AD∥OC,
∴∠DAC=∠ACO,
∵OA=OC,
∴∠OCA=∠OAC,
∴∠DAE=2α,
∵∠D=90°,
∴∠DAE+∠E=90°,
∴2α+β=90°(0°<α<45°)
(2)解:连接OF交AC于O′,连接CF.

∵AO′=CO′,
∴AC⊥OF,
∴FA=FC,
∴∠FAC=∠FCA=∠CAO,
∴CF∥OA,∵AF∥OC,
∴四边形AFCO是平行四边形,
∵OA=OC,
∴四边形AFCO是菱形,
∴AF=AO=OF,
∴△AOF是等边三角形,
∴∠FAO=2α=60°,
∴α=30°,
∵2α+β=90°,
∴β=30°,
∴α=β=30°.
【解析】(1)首先证明∠DAE=2α,在Rt△ADE中,根据两锐角互余,可知2α+β=90°,(0°<α<45°);(2)连接OF交AC于O′,连接CF.只要证明四边形AFCO是菱形,推出△AFO是等边三角形即可解决问题;


科目:初中数学 来源: 题型:
【题目】
(1)如果点P到点A,点B的距离相等,那么x=______;
(2)当x=______时,点P到点A,点B的距离之和是6;
(3)若点P到点A,点B的距离之和最小,则x的取值范围是______;
(4)在数轴上,点M,N表示的数分别为x![]() ,x
,x![]() ,我们把x
,我们把x![]() ,x
,x![]() 之差的绝对值叫做点M,N之间的距离,即MN="|" x
之差的绝对值叫做点M,N之间的距离,即MN="|" x![]() -x
-x![]() |.若点P以每秒3个单位长度的速度从点O沿着数轴的负方向运动时,点E以每秒1个单位长度的速度从点A沿着数轴的负方向运动、点F以每秒4个单位长度的速度从点B沿着数轴的负方向运动,且三个点同时出发,那么运动______秒时,点P到点E,点F的距离相等.
|.若点P以每秒3个单位长度的速度从点O沿着数轴的负方向运动时,点E以每秒1个单位长度的速度从点A沿着数轴的负方向运动、点F以每秒4个单位长度的速度从点B沿着数轴的负方向运动,且三个点同时出发,那么运动______秒时,点P到点E,点F的距离相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
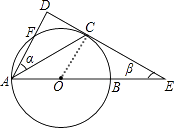
【题目】已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作: 将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M间的距离可能是( )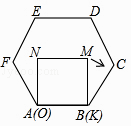
A.1.4
B.1.1
C.0.8
D.0.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大小不同的两个磁块,其截面都是等边三角形,小三角形边长是大三角形边长的一半,点O是小三角形的内心,现将小三角形沿着大三角形的边缘顺时针滚动,当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是( ) 
A.240°
B.360°
C.480°
D.540°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解
如图1,已知点A是BC外一点,连接AB,AC,求∠BAC+∠B+∠C的度数.
(1)阅读并补充下面推理过程
解:过点A作ED∥BC
∴∠B=∠ ,∠C=∠ .
又∵∠EAB+∠BAC+∠DAC=180°(平角定义)
∴∠B+∠BAC+∠C=180°
从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将∠BAC,∠B,∠C“凑”在一起,得出角之间的关系,使问题得以解决
(2)如图2,已知AB∥ED,求∠B+∠BCD+∠D的度数.
小明受到启发,过点C作CF∥AB如图所示,请你帮助小明完成解答:
(3)已知AB∥CD,点C在点D的右侧,∠ADC=70°.BE平分∠ABC,DE平分∠ADC,BE,DE所在的直线交于点E,点E在AB与CD两条平行线之间.
①如图3,点B在点A的左侧,若∠ABC=60°,则∠BED的度数为 °.
②如图4,点B在点A的右侧,且AB<CD,AD<BC.若∠ABC=n°,则∠BED的度数为 °(用含n的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+5(k1<0)的图象与坐标轴交于A,B两点,与反比例函数y= ![]() (k2>0)的图象交于M,N两点,过点M作MC⊥y轴于点C,已知CM=1.
(k2>0)的图象交于M,N两点,过点M作MC⊥y轴于点C,已知CM=1.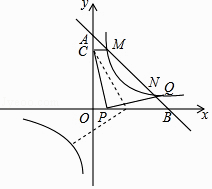
(1)求k2﹣k1的值;
(2)若 ![]() =
= ![]() ,求反比例函数的解析式;
,求反比例函数的解析式;
(3)在(2)的条件下,设点P是x轴(除原点O外)上一点,将线段CP绕点P按顺时针或逆时针旋转90°得到线段PQ,当点P滑动时,点Q能否在反比例函数的图象上?如果能,求出所有的点Q的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线![]() (x>0)交于D点,过点D作DC⊥x轴,垂足为G,连接OD.已知△AOB≌△ACD.
(x>0)交于D点,过点D作DC⊥x轴,垂足为G,连接OD.已知△AOB≌△ACD.
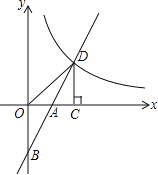
(1)如果b=﹣2,求k的值;
(2)试探究k与b的数量关系,并写出直线OD的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电销售商场电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商场用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)现在商场准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13200元,请分析合理的方案共有多少种?并确定获利最大的方案以及最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为坐标原点,我们把横、纵坐标都为整数的点称为整点,记定点都是整点的三角形为整点三角形.如图,已知整点O(0,0),A(2,4),请在所给网格区域(含边界)上按要求画图.
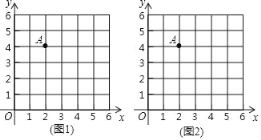
(1)在图1中画一个整点三角形OAB,其中点B在第一象限,且点B的横、纵坐标之和等于点A的横坐标;
(2)在图2中画一个整点三角形OAC,其中点C的坐标为(3t,t),且点C的横、纵坐标之和是点A的纵坐标的2倍.请直接写出△OAC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com