
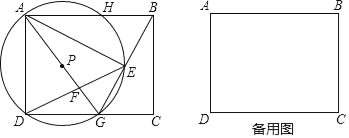
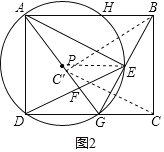
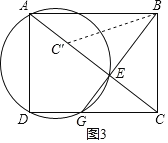
����Ŀ����֪����ABCD��AB=10��AD=8��GΪ��DC������һ�㣬����AG��BG����AGΪֱ������P�ֱ�BG��AB�ڵ�E��H������AE��DE��
��1������EΪ��GH���е㣬֤����AG=AB��
��2������ADEΪ����������ʱ����DG�ij���
��3������C����ֱ��BG�ĶԳƵ�C����
������C�����߶�AG��ʱ�����߶�AG��DE���ڵ�F������ADF����AEF�����֮�ȣ�
���ڵ�G���˶������У�����C�������ı���ADGE��ʱ���������߽磩����DG�ķ�Χ���� ����ֱ��д���𰸣�
���𰸡���1������������2��DG��4��6��5����3����![]() ����
����![]() ��DG��10��
��DG��10��
��������
��1����AGΪ��Pֱ���ɵã���AEG=��AEB=90�㣬�ɵ�EΪ��DH���е㣬�ɵã���BAE=��GAE���ɴ���֤����AEB�ա�AEG��
��2����ADEΪ���������Σ�Ҫ�������ۣ���AE=AD����AE=DE����AD=DE��
��3���١�ADF���AEF�ĸ���ȣ����֮�ȵ��ڵ�֮�ȣ�����PE��֤��PE��CD��������������������������ý��ۣ��ڵ�C'����AE��ʱ�����DG����Сֵ�����ֵ��������Ϊ10��
��1����AGΪ��Pֱ����
���AEG=��AEB=90�㣮
�ߵ�EΪ��DH���е㣬
���BAE=��GAE��
�ڡ�AEB�͡�AEG�У�
�� ��
��
���AEB�ա�AEG��ASA����
��AG=AB��
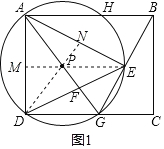
��2����ͼ1����ADEΪ���������Σ������������
��AE=AD=8��
��AGΪ��Pֱ����
���AEG=��AEB=90�㣬
��BE![]() 6��
6��
��ABCD�Ǿ��Σ�
���ABC=��BCD=��BAD=��ADC=90�㣬BC=AD=8��CD=AB=10��
���ABE+��CBG=90�㣬��BAE+��ABE=90�㣬
���CBG=��BAE��
�ڡ�BCG�͡�AEB�У�
�� ��
��
���BCG�ա�AEB��ASA����
��CG=BE=6��
��DG=CD��CG=10��6=4��
��AE=DE������E��EM��AD��M��
��AE=DE��EM��AD��
���AEM=��DEM����AME=��DME=90�㣬
��AB��CD��EM��
���BAE=��AEM=��DEM=��EDG��
��![]() ��
��
�ɣ�1����AG=AB=10��
��DG![]() 6��
6��
��AD=DE����D��DN��AE��N��
���AND=��AEB=90�㣬AN=NE��
�ߡ�DAE+��BAE=��ADN+��DAE=90�㣬
���BAE=��ADN��
���ADN�ס�BAE��
��![]() ��
��
����![]() ��
��
��![]() ��
��
�ߡ�ABE+��CBG=��CGB+��CBG=90�㣬
���ABE=��CGB��
�ߡ�AEB=��BCG=90�㣬
���BCG��AEB��
��![]() ��
��
����![]() ��
��
��CG=5��
��DG=CD��CG=10��5=5��
����������DG=4��6��5��
��3������ͼ2����C'��C����ֱ��BG�Գƣ�����BC'������PE������Գ����ʵã�BC'=BC����C'BG=��CBG��GC=GC'����BGC'=��BGC��
���BC'G=��BCG=90�㣬
���AC'B=��GDA=90�㣮
��AB��DC��
���BAC'=��AGD��
��BC'=BC=AD��
���ABC'�ա�GAD��AAS����
��AG=AB=10��DG![]() 6��
6��
��AB��CD��
���BGC=��ABG=��AGB��
��AE��BG��
��BE=EG��
��AP=PG��
��PE��AB��CD��PE![]() AB=5��
AB=5��
���DFG�ס�EFP��
��![]() ��
��
��![]() ��
��
����ͼ3������C'���ھ���ABCD�Խ���AC��ʱ��
�ߡ�AEB=��BEC=��ABC=��BCG=90�㣬
���BAC+��ACB=��CBG+��ACB=90�㣬
���BAC=��CBG��
���ABC�ס�BCG��
��![]() ��
��
��CG![]() ��
��
��DG=CD��CG=10![]() ��
��
����G�����˶��Ҳ����Cʱ��C'ʼ�������ı���ADGE�ڲ���
��DG��10��
��![]() DG��10��
DG��10��
�ʴ�Ϊ��![]() DG��10��
DG��10��


 �ŵ������ϵ�д�
�ŵ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����O����ֱ��AD�ĶԳƵ���E������AE��DE��
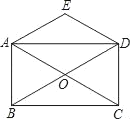
��1�����ж��ı���AODE����״������˵�����ɣ�
��2����������EB��EC����֤��EB��EC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��AOB�ǵȱ������Σ���A�������ǣ�0��4������B��һ���ޣ���P��t��0����x���ϵ�һ�����㣬����AP��������AOP���ŵ�A����ʱ�뷽����ת��ʹ��AO��AB�غϣ�����OD��PD������OPD��
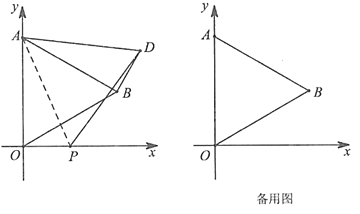
��1����t��![]() ʱ����DP�ij�
ʱ����DP�ij�
��2���ڵ�P�˶������У������������γɵ���OPD���ΪS
�ٵ�t��0ʱ����S��t֮��ĺ�����ϵʽ
�ڵ�t��0ʱ��Ҫʹs��![]() ����ֱ��д�����з��������ĵ�P������.
����ֱ��д�����з��������ĵ�P������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ı��ε�һ���Խ��߰��ı��ηֳ��������������Σ��������Խ��߽�������ı��ε����ɷ�����������ı��ν��������ı���������һ���ı����������ɷ��ߣ����Ϊ�������ı��Σ�
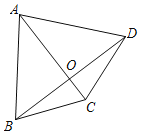
��1�������ı���һ���������ı��ε����� ��������ţ�
��ƽ���ı��Σ��ھ��Σ������Σ��������Σ�
������Ӧ�ã�
��2����ͼ���ھ����ı���ABCD�У�AC��AD����AC��ֱƽ��BD������BAD��80�������BCD�Ķ�����
���������
��3���������ı���ABCD�У�AB��AD��CD����A��90����AC���ı���ABCD���ɷ��ߣ���ֱ��д����BCD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC����A��90�㣬����C��CE��BD��BD�ڵ�E����CE��AB��
��1����֤����ABD�ա�ECB��
��2����AB��AD�����ADC�Ķ�����
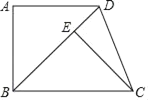
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ٵ��ˣ�����ӭ���ֻ��г�������������ij�̳����ۼס�������Ʒ�Ƶ������ֻ����������ֻ��Ľ��ۺ��ۼ����±���ʾ��
�� | �� | |
���ۣ�Ԫ/���� | 4000 | 2500 |
�ۼۣ�Ԫ/���� | 4300 | 3000 |
���̳��ƻ�Ͷ��15.5��Ԫ�ʽ�ȫ�����ڹ��������ֻ����ɲ�������ȫ�����ۺ�ɻ�ë������2��Ԫ����ë����=���ۼ۩����ۣ�����������
��1�����̳�Ҫ�뾡���ܶ�Ĺ��������ֻ���Ӧ�ð��������Ľ��������������������ֻ���
��2��ͨ���г����У����̳������ڼ����ֻ��������ķ����ϣ����ټ����ֻ��Ĺ������������������ֻ��Ĺ�����������֪�����ֻ����ӵ������Ǽ����ֻ����ٵ�������2�����������ڹ����������ֻ������ʽ���16��Ԫ�����̳�����������ʹȫ�����ۺ��õ�ë�������������ë����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��Ӧ�������Ļ����������٣�ijУ��չ�˹�ʫ���ж���������������ȡ����ͬѧ�ijɼ�����ͳ�ƣ������Ƴ����µ�������������ͳ��ͼ������ͼ���ṩ����Ϣ��������и��⣺
��1��ֱ��д��a��ֵ��a=�� ��������Ƶ���ֲ�ֱ��ͼ����������
��2��������B��Բ�ĽǶ�����
��3�����ȫУ��2000��ѧ���μ���λ��90�����ϣ���90�֣�Ϊ���㣬��ô���ƻ�����㽱��ѧ���ж����ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����Rt��ABC�У���A=90�㣬AB=AC����D��E�ֱ��ڱ�AB��AC�ϣ�AD=AE������DC����M��P��N�ֱ�ΪDE��DC��BC���е㣮
��1���۲����
ͼ1�У��߶�PM��PN��������ϵ�� ��λ�ù�ϵ�� ��
��2��̽��֤��
����ADE�Ƶ�A��ʱ�뷽����ת��ͼ2��λ�ã�����MN��BD��CE���ж���PMN����״����˵�����ɣ�
��3����չ����
����ADE�Ƶ�A��ƽ����������ת����AD=4��AB=10����ֱ��д����PMN��������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() �뷴��������
�뷴��������![]() ��ͼ����A��1��4����B��4��n�����㣮
��ͼ����A��1��4����B��4��n�����㣮

��1������������һ�κ����Ľ���ʽ��
��2��ֱ��д����x��0ʱ��![]() �Ľ⼯��
�Ľ⼯��
��3����P��x���ϵ�һ���㣬��ȷ����P������������꣬ʹPA+PB��С��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com