
【题目】如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( ) 
A.12
B.24
C.12 ![]()
D.16 ![]()
【答案】D
【解析】解:在矩形ABCD中,
∵AD∥BC,
∴∠DEF=∠EFB=60°,
∵把矩形ABCD沿EF翻折点B恰好落在AD边的B′处,
∴∠DEF=∠EFB=60°,∠B=∠A′B′F=90°,∠A=∠A′=90°,AE=A′E=2,
AB=A′B′,
在△EFB′中,
∵∠DEF=∠EFB=∠EB′F=60°
∴△EFB′是等边三角形,
Rt△A′EB′中,
∵∠A′B′E=90°﹣60°=30°,
∴B′E=2A′E,而A′E=2,
∴B′E=4,
∴A′B′=2 ![]() ,即AB=2
,即AB=2 ![]() ,
,
∵AE=2,DE=6,
∴AD=AE+DE=2+6=8,
∴矩形ABCD的面积=ABAD=2 ![]() ×8=16
×8=16 ![]() .
.
故选D.
解:在矩形ABCD中根据AD∥BC得出∠DEF=∠EFB=60°,由于把矩形ABCD沿EF翻折点B恰好落在AD边的B′处,
所以∠EFB=∠DEF=60°,∠B=∠A′B′F=90°,∠A=∠A′=90°,AE=A′E=2,AB=A′B′,
在△EFB′中可知∠DEF=∠EFB=∠EB′F=60°故△EFB′是等边三角形,由此可得出∠A′B′E=90°﹣60°=30°,根据直角三角形的性质得出A′B′=AB=2 ![]() ,然后根据矩形的面积公式列式计算即可得解.
,然后根据矩形的面积公式列式计算即可得解.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案科目:初中数学 来源: 题型:
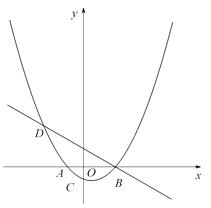
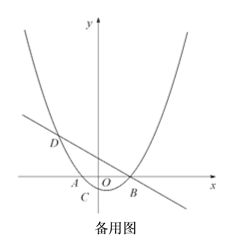
【题目】如图,已知抛物线![]() (a为常数,且a>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线
(a为常数,且a>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线![]() 与抛物线的另一交点为D,且点D的横坐标为﹣5.
与抛物线的另一交点为D,且点D的横坐标为﹣5.
(1)求抛物线的函数表达式;
(2)P为直线BD下方的抛物线上的一点,连接PD、PB, 求△PBD面积的最大值.
(3)设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小傅某天下午营运全是在东西走向的大道上行驶的,如果规定向东为正,行车里程(单位:km)如下:
+11, -2, +3, +9, -11, +5, -15, -8
(1)当把最后一名乘客送到目的地时,小傅距离出车地点的距离为多少?
(2)若每千米的营运额为5元,成本为2.7元/km,则这天下午他盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·柳州)在平面直角坐标系中,将点A (-2,1)向左平移2个单位到点Q,则点Q的坐标为
A.(-2,3)B.(0,1)C.(-4,1)D.(-4,-1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将函数y=﹣3x的图象沿y轴向上平移2个单位长度后,所得图象对应的函数关系式为( )
A.y=﹣3x+2
B.y=﹣3x﹣2
C.y=﹣3(x+2)
D.y=﹣3(x﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中错误的是( )

A. b2>4ac
B. ax2+bx+c≥﹣6
C. 若点(﹣2,m),(﹣5,n)在抛物线上,则m>n
D. 关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com