
分析 分两种情况:①点P在圆内,过点P作直径CD,如图1,根据相交弦定理得PA•PB=PC•PD,由于而PC=R-OP,PD=R+OP,则PA•PB=(R-OP)(R+OP),然后利用平方差公式展开即可得到结论;
点P在圆外,直线OP交⊙O于C、D,如图2,根据切割线定理得到PA•PB=PC•PD,由于PC=OP-R,PD=OP+R,则PA•PB=(OP-R)(OP+R)=OP2-R2,然后利用平方差公式展开即可得到结论.
解答 证明:①点P在圆内,过点P作直径CD,如图1,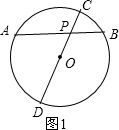
∵PA•PB=PC•PD,
而PC=OC-OP=R-OP,PD=OD+OP=R+OP,
∴PA•PB=(R-OP)(R+OP)=R2-OP2;
②点P在圆外,直线OP交⊙O于C、D,如图2,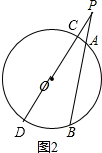
∵PCD和PAB都为⊙O的割线,
∴PA•PB=PC•PD,
而PC=OC-OP=OP-R,PD=OD+OP=OP+R,
∴PA•PB=(OP-R)(OP+R)=OP2-R2.
综上所述:PA•PB=|R2-OP2|.
点评 本题考查了切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.推论:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等. 也考查了相交弦定理.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
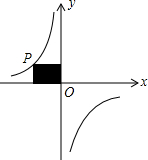 如图,P是反比例函数y=$\frac{k}{x}$的图象上的一点,过点P分别作x轴、y轴的垂线,得图中阴影部分的面积为6,则这个反比例函数的比例系数是-6.
如图,P是反比例函数y=$\frac{k}{x}$的图象上的一点,过点P分别作x轴、y轴的垂线,得图中阴影部分的面积为6,则这个反比例函数的比例系数是-6.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com