
分析 根据题意画出图形,通过解直角三角形用R分别表示出它们的边长,进而可得出结论.
解答 解:如图①所示,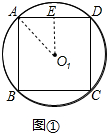 连接O1 A,作O1 E⊥AD于E,
连接O1 A,作O1 E⊥AD于E,
∵O1 A=R,∠O1 AE=45°,
∴AE=O1 A•cos45°=$\frac{\sqrt{2}}{2}$R,
∴AD=2AE=$\sqrt{2}$R;
如图②所示:
连接O2 A,O2 B,
则O2 B⊥AC,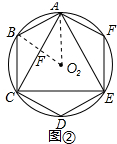
∵O2 A=R,∠O2 AF=30°,∠AO2 B=60°,
∴△AO2 B是等边三角形,AF=O2A•cos30°=$\frac{\sqrt{3}}{2}$R,
∴AB=R,AC=2AF=$\sqrt{3}$R;
∴圆内接正三角形、正四边形、正六边形的边长之比$\sqrt{3}$R:$\sqrt{2}$R:R=$\sqrt{3}$:$\sqrt{2}$:1.
点评 本题考查的是正多边形和圆、解直角三角形;熟知正三角形、正方形和正六边形的性质是解答此题的关键.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
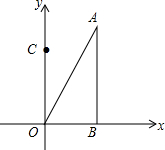 如图,Rt△ABO在平面直角坐标系中,O为原点,OB在x轴上,∠AOB=60°,点A坐标为(3,3$\sqrt{3}$),点C的坐标为(0,3),点D在第二象限,且△ABO≌△DCO.
如图,Rt△ABO在平面直角坐标系中,O为原点,OB在x轴上,∠AOB=60°,点A坐标为(3,3$\sqrt{3}$),点C的坐标为(0,3),点D在第二象限,且△ABO≌△DCO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
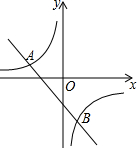 如图,已知一次函数y=kx+b的图象与反比例函数$y=-\frac{8}{x}$的图象交于A、B两点,且点A的纵坐标和点B的横坐标都是2.求:
如图,已知一次函数y=kx+b的图象与反比例函数$y=-\frac{8}{x}$的图象交于A、B两点,且点A的纵坐标和点B的横坐标都是2.求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10 | B. | 48 | C. | 36 | D. | 10或8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com