
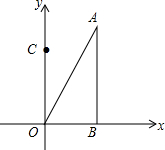
 如图,Rt△ABO在平面直角坐标系中,O为原点,OB在x轴上,∠AOB=60°,点A坐标为(3,3$\sqrt{3}$),点C的坐标为(0,3),点D在第二象限,且△ABO≌△DCO.
如图,Rt△ABO在平面直角坐标系中,O为原点,OB在x轴上,∠AOB=60°,点A坐标为(3,3$\sqrt{3}$),点C的坐标为(0,3),点D在第二象限,且△ABO≌△DCO.分析 (1)由△ABO≌△DCO,利用全等三角形的性质可得CD=BA,由点A坐标为(3,3$\sqrt{3}$),点C的坐标为(0,3),可得D点的坐标;
(2)首先利用全等三角形的性质可得OC=OB=3,∠BOC=90°,易得∠OBC=45°,分类讨论当CD为直角边时,过点D作P1D⊥CD,交BC于点P1,由DC∥OB,可得
△P1DC为等腰直角三角形,易得${P}_{1}D=DC=3\sqrt{3}$,可得P1点的坐标;当CD为斜边时,过D点作DP2⊥BC交BC于点P2,易得△CDP2是等腰直角三角形,作P2E⊥CD,可得CE=DE=$\frac{1}{2}CD$=$\frac{3\sqrt{3}}{2}$,易得P2点的坐标.
解答 解:(1)点D在第二象限,正确画出△COD如图所示,
∵△ABO≌△DCO,
∴CD=BA,
∵点A坐标为(3,3$\sqrt{3}$),点C的坐标为(0,3),
∴D(-3$\sqrt{3}$,3),
故答案为:(-3$\sqrt{3}$,3);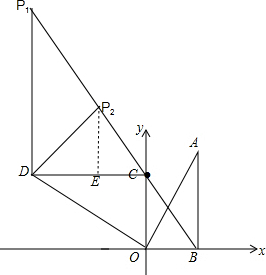
(2)∵OC=OB=3,∠BOC=90°,
∴∠OBC=45°,
①当CD为直角边时,如图,过点D作P1D⊥CD,交BC于点P1,
∵DC∥OB,
∴∠DCP1=∠OBC=45°,
∴△P1DC为等腰直角三角形,
∴${P}_{1}D=DC=3\sqrt{3}$,
∴P1(-3$\sqrt{3}$,3$+3\sqrt{3}$);
②当CD为斜边时,过D点作DP2⊥BC交BC于点P2,
易得△CDP2是等腰直角三角形,作P2E⊥CD,
∵CP2=DP2,
∴CE=DE=$\frac{1}{2}CD$=$\frac{3\sqrt{3}}{2}$,
∴P2($-\frac{3\sqrt{3}}{2}$,3$+\frac{3\sqrt{3}}{2}$).
综上所述,点P在直线BC上,使△PCD是等腰直角三角形的点P的坐标为($-3\sqrt{3}$,3$+3\sqrt{3}$),($-\frac{3\sqrt{3}}{2},3+\frac{3\sqrt{3}}{2}$).
点评 本题主要考查了全等三角形的性质和等腰直角三角形的性质,利用全等三角形的性质判断∠OBC=45°,分类讨论是解答此题的关键.


科目:初中数学 来源: 题型:解答题
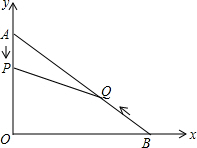 如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
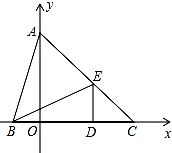 如图,在平面直角坐标系中,点A(0,b),点B(a,0),点D(d,0),其中a、b、d满足$\sqrt{a+1}$+|b-3|+(2-d)2=0,DE⊥x轴,且∠BED=∠ABO,直线AE交x轴于点C.
如图,在平面直角坐标系中,点A(0,b),点B(a,0),点D(d,0),其中a、b、d满足$\sqrt{a+1}$+|b-3|+(2-d)2=0,DE⊥x轴,且∠BED=∠ABO,直线AE交x轴于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
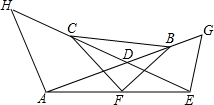 如图,已知AG与HE相交于点D,点B、C、F分别是DG、HD、AE的中点,若AH=AD,DE=EG.
如图,已知AG与HE相交于点D,点B、C、F分别是DG、HD、AE的中点,若AH=AD,DE=EG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com