
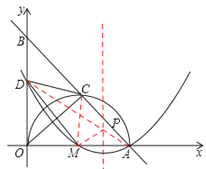
����Ŀ����ͼ����ֱ����ϵ�У�ֱ��AB��x���ڵ�A��5��0������y���ڵ�B��AO����M��ֱ�������Բ��AB�ڵ�C����AC=3��ȡBO���е�D������CD��MD��OC��

��1����֤��CD����M�����ߣ�
��2�����κ�����ͼ����D��M��A����Գ�������һ����P������PD��PM������PDM���ܳ���Сʱ��P�����ꣻ
��3���ڣ�2���������£�����PDM���ܳ���Сʱ�����������Ƿ���ڵ�Q��ʹ![]() �������ڣ������Q�����ꣻ�������ڣ���˵�����ɡ�
�������ڣ������Q�����ꣻ�������ڣ���˵�����ɡ�
���𰸡��⣺��1��֤��������CM��
��OA Ϊ��Mֱ�������OCA=90�㡣���OCB=90����
��DΪOB�е�����DC=DO�����DCO=��DOC��
��MO=MC�����MCO=��MOC��
��![]() ��
��
������C����M�ϣ���DC����M��������
��2����A�����꣨5��0����AC=3
����Rt��ACO����![]() ��
��
��![]() ����
����![]() �����
����� ![]() ��
��
����DΪOB�е㣬��![]() ����D������Ϊ��0��
����D��������0��![]() )��
)��
����AD����ֱ��AD�Ľ���ʽΪy=kx+b������
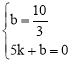 ���
���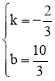 ��
��
��ֱ��ADΪ![]() ��
��
�����κ�����ͼ���M��![]() ��0)��A(5��0)��
��0)��A(5��0)��
�������߶Գ���x=![]() ��
��
����M��A����ֱ��x=![]() �Գƣ���ֱ��AD��ֱ��x=
�Գƣ���ֱ��AD��ֱ��x=![]() ���ڵ�P��
���ڵ�P��
��PD+PMΪ��С��
����DMΪ�����������������ĵ�PΪֱ��AD��ֱ��x=![]() �Ľ�����
�Ľ�����
��x=![]() ʱ��
ʱ��![]() ��
��
��P���������![]() ��
��![]() ����
����
��3��������
��![]() ��
��![]()
���ɣ�2��֪D��0��![]() )��P��
)��P��![]() ��
��![]() ����
����
����![]() ����
����![]() �����yQ=��
�����yQ=��![]() ��
��
�����κ�����ͼ���M(0��![]() )��A(5��0����
)��A(5��0����
������κ�������ʽΪ![]() ��
��
������ͼ�����D��0��![]() )����
)����![]() �����a=
�����a=![]() ��
��
�����κ�������ʽΪ![]() ��
��
����Q�����������ϣ���yQ=��![]() ��
��
����yQ=![]() ʱ��
ʱ��![]() �����x=
�����x=![]() ��x=
��x=![]() ��
��
��yQ=![]() ʱ��
ʱ��![]() �����x=
�����x=![]() ��
��
����Q��������![]() ��
��![]() )����
)����![]() ��
��![]() )����
)����![]() ��
��![]() ����
����
��������
�����������1������CM�����Եó�CM=OM��������MOC=��MCO����OAΪֱ����������ACO=90�㣬DΪOB���е㣬����CD=OD����DOC=��DCO������DOC+��MOC=90��Ϳ��Եó���DCO+��MCO=90����ó����ۡ�
��2�������������Եó�![]() ��
��![]() ���Ӷ����OB��ֵ������D��OB���е�Ϳ������D�����꣬�ɴ���ϵ�����Ϳ�����������ߵĽ���ʽ������Գ��ᣬ������ԳƵ���������AD���Գ�����P�������AD�Ľ���ʽ�Ϳ������P�����ꡣ
���Ӷ����OB��ֵ������D��OB���е�Ϳ������D�����꣬�ɴ���ϵ�����Ϳ�����������ߵĽ���ʽ������Գ��ᣬ������ԳƵ���������AD���Գ�����P�������AD�Ľ���ʽ�Ϳ������P�����ꡣ
��3������![]() ��
��![]() ���Q�������꣬������κ�������ʽ������ú����ꡣ
���Q�������꣬������κ�������ʽ������ú����ꡣ


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y��(1��m)x��ͼ����������A(x1��y1)��B(x2��y2)���ҵ�x1��x2ʱ��y1��y2����m��ȡֵ��Χ��( )
A. m��0 B. m��0 C. m��1 D. m��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���ABCD�У�AD��BC����C=90�㣬P��CD��һ�㣬BH��AP��H��BH=BC=CD 
��1����֤����ABP=45�㣻
��2����BC=20��PC=12����AP�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����m>n��km>kn����������Ϊ(����)
A. k>0 B. k<0 C. k��0 D. k��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijˮ�����������㽶������ǧ�ˣ����ۼۣ�Ԫ��֮��Ĺ�ϵ�����
������ǧ�ˣ� | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | �� |
�ۼۣ�Ԫ�� | 1.5 | 3 | 4.5 | 6 | 7.5 | 9 | 10.5 | �� |
�ϱ���ӳ��������֮��Ĺ�ϵ�����У��Ա�������������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����ɫ�����Ĵ�����װ�г���ɫ�������ͬ��7�������3��������ô���������������һ������Ŀ����Ժ�����һ������Ŀ�������ȣ�������
A. ����һ������Ŀ����Դ� B. ����һ������Ŀ����Դ�
C. ���ֿ�����һ���� D. ��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�BD��BE�ֱ��Ǹߺͽ�ƽ���ߣ���F��CA���ӳ����ϣ�FH��BE����BD�ڵ�G����BC�ڵ�H�����н��ۣ�
�١�DBE=��F��
��2��BEF=��BAF+��C��
�ۡ�F=��BAC����C��
�ܡ�BGH=��ABE+��C��
������ȷ�Ľ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����3��Я��������ϳ������ݣ���3�˵����ع�210kg�����y������20kg���������Ϊ1050kg����õ����ڴ�3�˳�������������ܴ���___���Ė���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com