
【题目】如图,已知四边形ABCD中,AD∥BC,∠C=90°,P是CD上一点,BH⊥AP于H,BH=BC=CD 
(1)求证:∠ABP=45°;
(2)若BC=20,PC=12,求AP的长.
【答案】
(1)证明:如图,作BE⊥DA于E,
∵AD∥BC,∠C=90°,
∴∠C+∠D=180°,
∴∠D=∠C=∠E=90°,
∴四边形BCDE是矩形,
∴BE=CD=BC=BH,
∵BH⊥AP,
∴∠AHB=∠BHP=90°,
在Rt△ABE和Rt△ABH中,
![]() ,
,
∴△ABE≌△ABH,
∴∠ABE=∠ABH,同理可证△PBH≌△PBC,
∴∠PBH=∠PBC,
∵∠EBC=90°,
∴2∠ABH+2∠PBH=90°,
∴∠ABH+∠PBH=45°,
∴∠ABP=45°
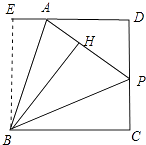
(2)证明:由(1)可知,四边形BCDE是矩形,
∵BC=CD,
∴四边形BCDE是正方形,
∴BC=CD=DE=BE=20,
∵△ABE≌△ABH,△PBH≌△PBC,
∴AE=AH,PC=PH,
∴AP=AE+PC,设AP=x,
则AE=x﹣12,AD=20﹣(x﹣12)=32﹣x,PD=8,
在Rt△ADP中,∵AD2+DP2=AP2,
∴(32﹣x)2+82=x2,
∴x=17,
∴AP=17.
【解析】(1)如图,作BE⊥DA于E,只要证明△ABE≌△ABH,△PBH≌△PBC,推出∠ABE=∠ABH,∠PBH=∠PBC,由∠EBC=90°,推出2∠ABH+2∠PBH=90°,由此即可证明.(2)首先证明AP=AE+PC,设PA=x,在Rt△ADP中,利用勾股定理列出方程即可解决问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,如图两幅图都是由同一副三角板拼凑得到的:
(1)图1中的∠ABC的度数为 .
(2)图2中已知AE∥BC,则∠AFD的度数为 . 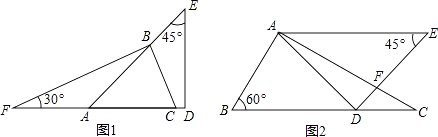
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名老师带领x名学生到动物园参观,已知成人票每张30元,学生票每张10元.设门票的总费用为y元,则y与x的函数关系为( )
A. y=10x+30 B. y=40x C. y=10+30x D. y=20x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=6,DH=2,平移距离为3,则阴影部分的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. 某事件发生的概率为1,则它必然会发生
B. 某事件发生的概率为0,则它必然不会发生
C. 抛一个普通纸杯,杯口不可能向上
D. 从一批产品中任取一个为次品是可能的
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角体系中,直线AB交x轴于点A(5,0),交y轴于点B,AO是⊙M的直径,其半圆交AB于点C,且AC=3。取BO的中点D,连接CD、MD和OC。

(1)求证:CD是⊙M的切线;
(2)二次函数的图象经过点D、M、A,其对称轴上有一动点P,连接PD、PM,求△PDM的周长最小时点P的坐标;
(3)在(2)的条件下,当△PDM的周长最小时,抛物线上是否存在点Q,使![]() ?若存在,求出点Q的坐标;若不存在,请说明理由。
?若存在,求出点Q的坐标;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com