
【题目】如图,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于A、B两点,点B的纵坐标为﹣1.过点A作
的图象交于A、B两点,点B的纵坐标为﹣1.过点A作![]() 轴于点C,且OC=1,
轴于点C,且OC=1,![]() 的面积为1.
的面积为1.
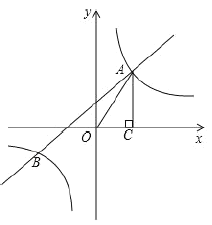
(1)求反比例函数和一次函数的表达式;
(2)若点D是反比例函数图象上的一点,且到点A、C的距离相等,求点D的坐标.
(3)结合图象直接写出当![]() 时,x的取值范围.
时,x的取值范围.
【答案】(1)![]() ,
,![]() ;(2)点D的坐标为(2,1);(3)
;(2)点D的坐标为(2,1);(3)![]() 或
或![]()
【解析】
(1)由△AOC的面积为1,OC=1,可得点A的横坐标为1,可求点A的纵坐标,确定反比例函数解析式,利用反比例函数解析式求B点坐标,利用“两点法”求一次函数解析式;
(2)由点D到点A、C的距离相等,可知D在AC的垂直平分线上,于是可求点D的纵坐标,再根据反比例函数图象上点的坐标特征即可求解;
(3)观察图象,直接写出即可.
解:(1)∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
即![]() ,
,
把A点坐标代入![]() 中,得
中,得![]() ,
,
∴![]() ,
,
∵点B的纵坐标为-1.
把![]() 代入
代入![]() 中,得
中,得![]() ,
,
∴![]() ,
,
将A、B两点坐标代入![]() ,
,
得![]() ,
,
解得![]() ,
,
∴![]() ;
;
(2)∵点D是反比例函数图象上的一点,且到点A、C的距离相等,
∴D在AC的垂直平分线上,
∴D的纵坐标为1,
当![]() 时,
时,![]() ,解得
,解得![]() .
.
故点D的坐标为(2,1).
(3)由图象可知,当![]() 时,
时,![]() 或
或![]() .
.


 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 与y轴交于C点,与x轴交于A,B两点(点A在点B左侧),且点A的横坐标为-1.
与y轴交于C点,与x轴交于A,B两点(点A在点B左侧),且点A的横坐标为-1.

(1)求a的值;
(2)设抛物线的顶点P关于原点的对称点为![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)将抛物线在A,B两点之间的部分(包括A, B两点),先向下平移3个单位,再向左平移m(![]() )个单位,平移后的图象记为图象G,若图象G与直线
)个单位,平移后的图象记为图象G,若图象G与直线![]() 无交点,求m的取值范围.
无交点,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,号称“千湖之省”的湖北正遭受大旱,为提高学生环境意识,节约用水,某校数学教师编制了一道应用题:为了保护水资源,某市制定一套节水的管理措施,其中对居民生活用水收费作如下规定:
月用水量(吨) | 单价(元/吨) |
不大于10吨部分 | 1.5 |
大于10吨不大于m吨部分(20≤m≤50) | 2 |
大于m吨部分 | 3 |
(1)若某用户六月份用水量为18吨,求其应缴纳的水费;
(2)记该用户六月份用水量为![]() 吨,缴纳水费为
吨,缴纳水费为![]() 元,试列出
元,试列出![]() 与
与![]() 的函数式;
的函数式;
(3)若该用户六月份用水量为40吨,缴纳水费![]() 元的取值范围为
元的取值范围为![]() ,试求
,试求![]() 的取值范围.
的取值范围.
各位同学,请你也认真做一做,相信聪明的你一定会顺利完成.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 过点
过点![]() ,顶点为M,与x轴交于AB两点,D为AB的中点,
,顶点为M,与x轴交于AB两点,D为AB的中点,![]() 轴,交抛物线于点E,下列结论中正确的是( )
轴,交抛物线于点E,下列结论中正确的是( )
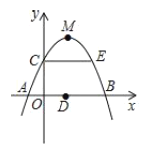
A.抛物线的对称轴是直线x=-3B.![]()
C.![]() D.四边形ADEC是菱形
D.四边形ADEC是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业在甲地又一工厂(简称甲厂)生产某产品,2017年的年产量过百万,2018年甲厂经过技术改造,日均生产的该产品数是该厂2017年的2倍还多2件.
(1)若甲厂2018年生产200件该产品所需的时间与2017年生产98件该产品所需的时间相同,则2017年甲厂日均生产该产品多少件?
(2)由于该产品深受顾客喜欢,2019年该企业在乙地建立新厂(简称乙厂)生产该产品,乙厂的日均生产的该产品数是甲厂2017年的3倍还要多5件,同年该企业要求甲、乙两厂分别生产m,n件产品(甲厂的日均产量与2018年相同),m:n=14:25,若甲、乙两厂同时开始生产,谁先完成任务?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
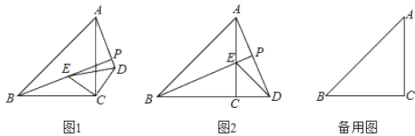
【题目】如图1,△ABC和△DEC均为等腰三角形,且∠ACB=∠DCE=90°,连接BE,AD,两条线段所在的直线交于点P.
(1)线段BE与AD有何数量关系和位置关系,请说明理由.
(2)若已知BC=12,DC=5,△DEC绕点C顺时针旋转,
①如图2,当点D恰好落在BC的延长线上时,求AP的长;
②在旋转一周的过程中,设△PAB的面积为S,求S的最值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:各类方程的解法
求解一元一次方程, 根据等式的基本性质,把方程转化为![]() 的形式;求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为二元一次方程组来解.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生不适合原方程的根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想-转化,即:把未知转化为已知.用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程可以通过因式分解把它转化为
的形式;求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为二元一次方程组来解.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生不适合原方程的根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想-转化,即:把未知转化为已知.用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程可以通过因式分解把它转化为![]() ,解方程
,解方程![]() 和
和![]() ,可得方程
,可得方程![]() 的解
的解
![]() 问题:方程
问题:方程![]() 的解是
的解是![]() ,
,![]() ,
,![]()
![]() 拓展:用“转化”思想求方程
拓展:用“转化”思想求方程![]() 的解;
的解;
![]() 变式:用“转化”思想解方程
变式:用“转化”思想解方程![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com