
【题目】阅读材料:各类方程的解法
求解一元一次方程, 根据等式的基本性质,把方程转化为![]() 的形式;求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为二元一次方程组来解.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生不适合原方程的根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想-转化,即:把未知转化为已知.用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程可以通过因式分解把它转化为
的形式;求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为二元一次方程组来解.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生不适合原方程的根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想-转化,即:把未知转化为已知.用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程可以通过因式分解把它转化为![]() ,解方程
,解方程![]() 和
和![]() ,可得方程
,可得方程![]() 的解
的解
![]() 问题:方程
问题:方程![]() 的解是
的解是![]() ,
,![]() ,
,![]()
![]() 拓展:用“转化”思想求方程
拓展:用“转化”思想求方程![]() 的解;
的解;
![]() 变式:用“转化”思想解方程
变式:用“转化”思想解方程![]() .
.
 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,点![]() 是等边
是等边![]() 内一点,且
内一点,且![]() ,点
,点![]() 是边
是边![]() 的中点,连接
的中点,连接![]() ,
,![]() .
.
(1)如图1,若点![]() ,
,![]() ,
,![]() 三点共线,则
三点共线,则![]() 与
与![]() 的数量关系是______;
的数量关系是______;
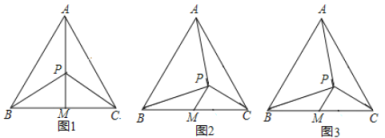
(2)如图2,若点![]() ,
,![]() ,
,![]() 三点不共线,问(1)中的结论还成立吗?若成立,请给出证明,若不成立,请说明理由;
三点不共线,问(1)中的结论还成立吗?若成立,请给出证明,若不成立,请说明理由;
(3)如图3,若![]() ,
,![]() ,直接写出
,直接写出![]() 的长是______.
的长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于A、B两点,点B的纵坐标为﹣1.过点A作
的图象交于A、B两点,点B的纵坐标为﹣1.过点A作![]() 轴于点C,且OC=1,
轴于点C,且OC=1,![]() 的面积为1.
的面积为1.
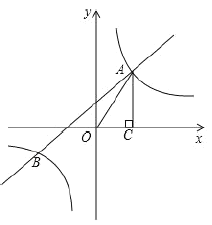
(1)求反比例函数和一次函数的表达式;
(2)若点D是反比例函数图象上的一点,且到点A、C的距离相等,求点D的坐标.
(3)结合图象直接写出当![]() 时,x的取值范围.
时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() 厘米,点
厘米,点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以每秒2厘米的速度移动,同时点
以每秒2厘米的速度移动,同时点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以每秒1厘米的速度移动,其中任意一点到达目的地后,两点同时停止运动.求:
以每秒1厘米的速度移动,其中任意一点到达目的地后,两点同时停止运动.求:
(1)点![]() 从点
从点![]() 出发,经过几秒
出发,经过几秒![]() 的面积等于1平方厘米?
的面积等于1平方厘米?
(2)是否存在以点![]() 为圆心、
为圆心、![]() 为半径的圆与直线
为半径的圆与直线![]() 相切,若存在,求出经过几秒相切?若不存在,请说明理由;
相切,若存在,求出经过几秒相切?若不存在,请说明理由;
(3)如图2,点![]() 是
是![]() 内的一个动点,且满足
内的一个动点,且满足![]() ,求线段
,求线段![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c的图象如图所示,对称轴为直线x=1.以下结论:①2a>-b;②4a+2b+c>0;③m(am+b)>a+b(m是大于1的实数);④3a+c<0其中正确结论的个数为( )
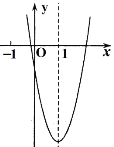
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西汾酒,又称“杏花村酒”.酿造汾酒是选用晋中平原的“一把抓高粱”为原料.汾阳县某村民合作社2016年种植“一把抓高粱”100亩,2018年该合作社扩大了“一把抓高梁”的种植面积,共种植144亩.
(1)求该合作社这两年种植“一把抓高梁”亩数的平均增长率;
(2)某粮店销售“一把抓高粱”售价为13元/斤,每天可售出30斤,每斤的盈利是1.5元.为了减少库存,粮店决定搞促销活动.在销售中发现:售价每降价0.1元,则可多售出2斤.若该粮店某天销售“一把抓高梁”的盈利为40元,则该店当天销售单价降低了多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF;其中正确的是( )
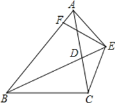
A.①②③B.①③④C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应党的“文化自信”号召,某校开展了古诗词诵读大赛活动,现随机抽取部分同学的成绩进行统计,并绘制成如下的两个不完整的统计图,请结合图中提供的信息,解答下列各题:
(1)直接写出a的值,a= ,并把频数分布直方图补充完整.
(2)求扇形B的圆心角度数.
(3)如果全校有2000名学生参加这次活动,90分以上(含90分)为优秀,那么估计获得优秀奖的学生有多少人?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com