
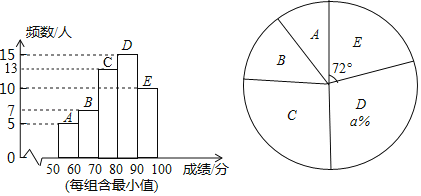
【题目】为响应党的“文化自信”号召,某校开展了古诗词诵读大赛活动,现随机抽取部分同学的成绩进行统计,并绘制成如下的两个不完整的统计图,请结合图中提供的信息,解答下列各题:
(1)直接写出a的值,a= ,并把频数分布直方图补充完整.
(2)求扇形B的圆心角度数.
(3)如果全校有2000名学生参加这次活动,90分以上(含90分)为优秀,那么估计获得优秀奖的学生有多少人?

【答案】(1)30,补图见解析;(2)扇形B的圆心角度数为50.4°;(3)估计获得优秀奖的学生有400人.
【解析】(1)先根据E等级人数及其占总人数的比例可得总人数,再用D等级人数除以总人数可得a的值,用总人数减去其他各等级人数求得C等级人数可补全图形;
(2)用360°乘以A等级人数所占比例可得;
(3)用总人数乘以样本中E等级人数所占比例.
(1)∵被调查的总人数为10÷![]() =50(人),
=50(人),
∴D等级人数所占百分比a%=![]() ×100%=30%,即a=30,
×100%=30%,即a=30,
C等级人数为50﹣(5+7+15+10)=13人,
补全图形如下:
故答案为:30;
(2)扇形B的圆心角度数为360°×![]() =50.4°;
=50.4°;
(3)估计获得优秀奖的学生有2000×![]() =400人.
=400人.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,为了测量河对岸l1上两棵古树A、B之间的距离,某数学兴趣小组在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则A、B之间的距离为( )
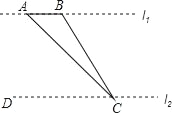
A. 50m B. 25m C. (50﹣![]() )m D. (50﹣25
)m D. (50﹣25![]() )m
)m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中:
①∠ABC=∠ADC;
②AC与BD相互平分;
③AC,BD分别平分四边形ABCD的两组对角;
④四边形ABCD的面积S=![]() ACBD.
ACBD.
正确的是________(填写所有正确结论的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(1,4),B(1,1),C(3,1).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出△ABC绕点O逆时针旋转90°后的△A2B2C2;
(3)在(2)的条件下,求线段BC扫过的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校未了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按![]() ,
,![]() ,
,![]() ,
,![]() 四个等级进行统计,制成了如下不完整的统计图.
四个等级进行统计,制成了如下不完整的统计图.

根据所给信息,解答以下问题
(1)在扇形统计图中,![]() 对应的扇形的圆心角是________度;
对应的扇形的圆心角是________度;
(2)补全条形统计图;
(3)该校九年级有300名学生,请估计足球运球测试成绩达到![]() 级的学生有多少人?
级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的边AB在x轴上,点B坐标(﹣3,0),点C在y轴正半轴上,且sin∠CBO=![]() ,点P从原点O出发,以每秒一个单位长度的速度沿x轴正方向移动,移动时间为t(0≤t≤5)秒,过点P作平行于y轴的直线l,直线l扫过四边形OCDA的面积为S.
,点P从原点O出发,以每秒一个单位长度的速度沿x轴正方向移动,移动时间为t(0≤t≤5)秒,过点P作平行于y轴的直线l,直线l扫过四边形OCDA的面积为S.
(1)求点D坐标.
(2)求S关于t的函数关系式.
(3)在直线l移动过程中,l上是否存在一点Q,使以B、C、Q为顶点的三角形是等腰直角三角形?若存在,直接写出Q点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为使中华传统文化教育更具有实效性,军宁中学开展以“我最喜爱的传统文化种类”为主题的调查活动,围绕“在诗词、国画、对联、书法、戏曲五种传统文化中,你最喜爱哪一种?(必选且只选一种)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题:
(1)本次调查共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)若军宁中学共有960名学生,请你估计该中学最喜爱国画的学生有多少名?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论错误的是
A. 全等三角形对应边上的中线相等
B. 两个直角三角形中,两个锐角相等,则这两个三角形全等
C. 全等三角形对应边上的高相等
D. 两个直角三角形中,斜边和一个锐角对应相等,则这两个三角形全等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com