
| A. | 1,$\sqrt{2}$,$\sqrt{3}$ | B. | 15,8,17 | C. | 13,14,15 | D. | $\frac{3}{5}$,$\frac{4}{5}$,1 |
分析 满足a2+b2=c2的三个正整数,称为勾股数,依此判断即可.
解答 解:A、∵1,$\sqrt{2}$,$\sqrt{3}$不都是整数,∴此选项不符合题意;
B、∵152+82=172,且15,8,17都是整数,∴此选项符合题意;
C、∵132+142≠152,∴此选项符合题意;
D、∵$\frac{3}{5}$,$\frac{4}{5}$,1不都是整数,∴此选项不符合题意.
故选B.
点评 本题考查了勾股数,注意:
①三个数必须是正整数,例如:2.5、6、6.5满足a2+b2=c2,但是它们不是正整数,所以它们不是够勾股数.
②一组勾股数扩大相同的整数倍得到三个数仍是一组勾股数.
③记住常用的勾股数再做题可以提高速度.如:3,4,5;6,8,10;5,12,13;…


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
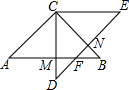 如图,△ABC中,∠ACB=90°,AC=BC=2$\sqrt{2}$,将△ABC绕着点C逆时针旋转45°后得到△DEC,AB、DE交于点F,CD交AB于M,CB交DE于N.
如图,△ABC中,∠ACB=90°,AC=BC=2$\sqrt{2}$,将△ABC绕着点C逆时针旋转45°后得到△DEC,AB、DE交于点F,CD交AB于M,CB交DE于N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
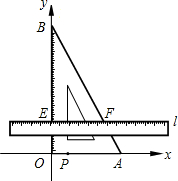 如图,把含有30°角的三角板ABO置入平面直角坐标系中,A,B两点坐标分别为(3,0)和(0,3$\sqrt{3}$).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动,速度分别为1,$\sqrt{3}$,2(长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以$\frac{\sqrt{3}}{3}$(长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
如图,把含有30°角的三角板ABO置入平面直角坐标系中,A,B两点坐标分别为(3,0)和(0,3$\sqrt{3}$).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动,速度分别为1,$\sqrt{3}$,2(长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以$\frac{\sqrt{3}}{3}$(长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
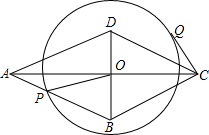 如图:已知菱形ABCD中,对角线AC和BD相交于点O,AC=8,BD=6,动点P在边AB上运动,以点O为圆心,OP为半径作⊙O,CQ切⊙O于点Q.则在点P运动过程中,切线CQ的长的最大值为$\frac{16}{5}$.
如图:已知菱形ABCD中,对角线AC和BD相交于点O,AC=8,BD=6,动点P在边AB上运动,以点O为圆心,OP为半径作⊙O,CQ切⊙O于点Q.则在点P运动过程中,切线CQ的长的最大值为$\frac{16}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{12}|a|b$ | B. | |a|$\sqrt{\frac{b}{12}}$ | C. | $\frac{a\sqrt{3b}}{6}$ | D. | -$\frac{a\sqrt{3b}}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com