
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,
,![]() 与
与![]() 的平分线交于
的平分线交于![]() 点,连接
点,连接![]() .
.
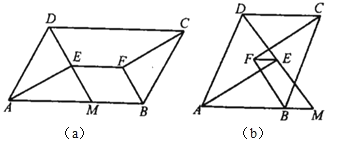
(1)延长![]() 交
交![]() 于
于![]() 点,则图(a)中与线段
点,则图(a)中与线段![]() 一定相等的线段有哪几条?说明理由(不再另外添加字母和辅助线).
一定相等的线段有哪几条?说明理由(不再另外添加字母和辅助线).
(2)![]() 、
、![]() 与
与![]() 之间有怎样的数量关系?为什么?
之间有怎样的数量关系?为什么?
(3)如果将条件“![]() ”改为“
”改为“![]() ”,如图(b)所示,其他条件不变,
”,如图(b)所示,其他条件不变,![]() 、
、![]() 与
与![]() 的关系又如何?直接写出结论.
的关系又如何?直接写出结论.
【答案】(1)与线段![]() 一定相等的线段有
一定相等的线段有![]() 和
和![]() ,理由见解析;(2)EF+BC=AB;(3)EF+AB=BC
,理由见解析;(2)EF+BC=AB;(3)EF+AB=BC
【解析】
(1)根据全等三角形的判定方法,结合题意可得: ![]() ;进而可得
;进而可得
DE=BF,ED=EM;(2)由(1)易得![]() 故
故![]() 进而可得根据平行线的性质可得EF=MB,BC=AD=AM,故有EF+BC=AB;(3)根据题意,利用(2)的方法,易得EFBM是平行四边形,由平行四边形的性质,易得答案.
进而可得根据平行线的性质可得EF=MB,BC=AD=AM,故有EF+BC=AB;(3)根据题意,利用(2)的方法,易得EFBM是平行四边形,由平行四边形的性质,易得答案.
(1)与线段![]() 一定相等的线段有
一定相等的线段有![]() 和
和![]() .
.
∵四边形![]() 是平行四边形,∴
是平行四边形,∴![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,![]() .
.
∵![]() 、
、![]() 分别平分
分别平分![]() 和
和![]() ,∴
,∴![]() ,
,
![]() ,∴
,∴![]() ,∴
,∴![]() .∴
.∴![]() .
.
∵![]() 分别平分
分别平分![]() ,∴
,∴![]() ,∴
,∴![]() .同理:
.同理:![]() .
.
∵![]() .∴
.∴![]() ,∴
,∴![]() ,∴
,∴![]() .
.
(2)![]() .
.
由(1)易证![]() ,∴
,∴![]() ,
,![]() ,∴四边形
,∴四边形![]() 是平行四边形,∴
是平行四边形,∴![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() .
.
(3)![]() .
.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】鼎丰超市以固定进价一次性购进保温杯若干个,11月份按一定售价销售,销售额为1800元,为扩大销量,减少库存,12月份在11月份售价基础上打9折销售,结果销售量增加50个,销售额增加630元.
(1)求鼎丰超市11月份这种保温杯的售价是多少元?
(2)如果鼎丰超市11月份销售这种保温杯的利润为600元,那么该鼎丰超市12月份销售这种保温杯的利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx(a≠0)过点E(10,0),矩形ABCD的边AB在线段OE上(点A在点B的左边),点C,D在抛物线上.设A(t,0),当t=2时,AD=4.
(1)求抛物线的函数表达式.
(2)当t为何值时,矩形ABCD的周长有最大值?最大值是多少?
(3)保持t=2时的矩形ABCD不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G,H,且直线GH平分矩形的面积时,求抛物线平移的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
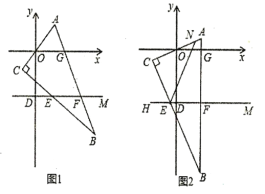
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 平行于
平行于![]() 轴并交
轴并交![]() 轴于
轴于![]() ,一块三角板摆放其中,其边与
,一块三角板摆放其中,其边与![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,与直线
两点,与直线![]() 分别交于
分别交于![]() ,
,![]() 两点,
两点,
(1)将三角板如图1所示的位置摆放,请写出![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(2)将三角板按如图2所示的位置摆放,![]() 为
为![]() 上一点,
上一点,![]() ,请写出
,请写出![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天,小华和小夏玩掷骰子游戏,他们约定:他们用同一枚质地均匀的骰子各掷一次, 如果两次掷的骰子的点数相同则小华获胜:如果两次掷的骰子的点数的和是6则小夏获胜.
(1)请您列表或画树状图列举出所有可能出现的结果;
(2)请你判断这个游戏对他们是否公平并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,横坐标为a的点A在反比例函数y1═![]() (x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
(x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
(1)设a=2,点B(4,2)在函数y1、y2的图象上.
①分别求函数y1、y2的表达式;
②直接写出使y1>y2>0成立的x的范围;
(2)如图①,设函数y1、y2的图象相交于点B,点B的横坐标为3a,△AA'B的面积为16,求k的值;
(3)设m=![]() ,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.
,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.

查看答案和解析>>
科目:初中数学 来源: 题型:
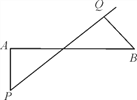
【题目】如图,B地在A地的正东方向,两地相距28![]() km.A,B两地之间有一条东北走向的高速公路,且A,B两地到这条高速公路的距离相等.上午8:00测得一辆在高速公路上行驶的汽车位于A地的正南方向P处,至上午8:20,B地发现该车在它的西北方向Q处,该段高速公路限速为110 km/h.问:该车是否超速行驶?
km.A,B两地之间有一条东北走向的高速公路,且A,B两地到这条高速公路的距离相等.上午8:00测得一辆在高速公路上行驶的汽车位于A地的正南方向P处,至上午8:20,B地发现该车在它的西北方向Q处,该段高速公路限速为110 km/h.问:该车是否超速行驶?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com