

分析 (1)如图1,延长AB到K,使AB=BK,连接DK,则有AK=2AB,由已知等式,将2AB代换为AK,利用两边对应成比例且夹角相等的三角形相似得到三角形ADK与三角形DMA相似,利用相似三角形对应角相等得到∠ADK为直角,利用直角三角形斜边上的中线等于斜边的一半即可得证;
(2)BF=BG+DG或BF=BG-DG,理由为:利用两对角相等的三角形相似得到三角形ABE与三角形CBA相似,由相似得比例,等量代换后利用两边对应成比例且夹角相等的三角形相似得到三角形BDE与三角形BCD相似,利用相似三角形对应角相等,得到四边形FBDC对角互补,即F,B,D,C四点共圆,利用同弧所对的圆周角相等得到一对角相等,等量代换后,利用等角对等边得到BF=BD,分两种情况考虑:当G在BD上与G在BD的延长线上,即可得证.
解答 (1)证明:如图1,延长AB到K,使AB=BK,连接DK,则有AK=2AB,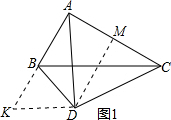
∵AD2=2AB×DM,
∴AD2=AK×DM,即$\frac{AD}{AK}$=$\frac{DM}{AD}$,
∵DM⊥AC,
∴∠DMC=∠BAC=90°,
∴AB∥DM,
∴∠KAD=∠ADM,
∴△ADK∽△DMA,
∴∠ADK=∠AMD=90°,
∴BD为斜边AB上的中线,
∴BD=BA;
(2)解:BF=BG+DG或BF=BG-DG,理由为:
∵AE⊥BC,
∴∠AEB=90°=∠BAC,
∵∠ABE=∠CBA,
∴△ABE∽△CBA,
∴$\frac{BE}{AB}$=$\frac{AB}{BC}$,
∵AB=BD,
∴$\frac{BE}{BD}$=$\frac{BD}{BC}$,
∵∠EBD=∠DBC,
∴△BDE∽△BCD,
∴∠BDE=∠BCD,
∵∠BCD=∠BCF,
∴∠BDE=∠BCF,
∴四边形FBDC对角互补,即F,B,D,C四点共圆,
∴∠BFD=∠BCD,
∴∠BDF=∠BFD,
∴BF=BD,
分两种情况考虑:
①如图2(1),当G在BD上时,BF=BG+DG;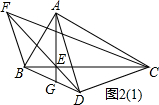
②如图2(2),当G在BD延长线上时,BF=BG-DG.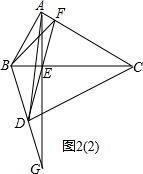
点评 此题属于相似形综合题,涉及的知识有:相似三角形的判定与性质,四点共圆的条件,圆周角定理,以及直角三角形斜边上的中线性质,熟练掌握相似三角形的判定与性质是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | Q=0.5t | B. | Q=15t | C. | Q=15+0.5t | D. | Q=15-0.5t |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
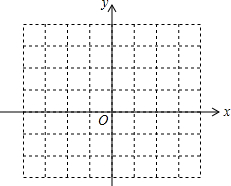 在平面直角坐标系中有一正方形网格,毎个小正方形的边长均为1,四边形各顶 点的坐标分别为A(1,1),B(3,1),C(3,2),D(2,3).
在平面直角坐标系中有一正方形网格,毎个小正方形的边长均为1,四边形各顶 点的坐标分别为A(1,1),B(3,1),C(3,2),D(2,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}-1}{2}$ | B. | $\frac{\sqrt{2}-\sqrt{6}}{4}$ | C. | $\frac{\sqrt{3}-1}{2}$ | D. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
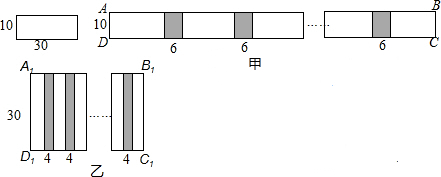
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com