
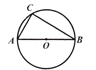
【题目】(10分)如图,⊙O是△ABC的外接圆,AB是⊙O的直径,AB=8.
(1)利用尺规,作∠CAB的平分线,交⊙O于点D;(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接CD,OD,若AC=CD,求∠B的度数;
(3)在(2)的条件下,OD交BC于点E.求出由线段ED,BE,![]() 所围成区域的面积.(其中
所围成区域的面积.(其中![]() 表示劣弧,结果保留π和根号)
表示劣弧,结果保留π和根号)
【答案】(1)作图见解析;(2)30°;(3)![]() .
.
【解析】
试题分析:(1)作AP平分∠CAB交⊙O于D;
(2)由等腰三角形性质得到∠CAD=∠ADC.又由∠ADC=∠B,得到∠CAD=∠B.
再根据角平分线定义得到∠CAD=∠DAB=∠B.由于直径所对圆周角为90°,得到∠ACB=90°,从而得到∠B的度数;
(3)先得到△OEB是30°角的直角三角形,从而得出OE,EB的长,然后把不规则图形面积转化为扇形BOD的面积减去Rt△OEB的面积求解.
试题解析:(1)如图,AP即为所求的∠CAB的平分线;
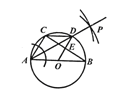
(2)∵AC=CD,∴∠CAD=∠ADC.又∵∠ADC=∠B,∴∠CAD=∠B.
∵AD平分∠CAB,∴∠CAD=∠DAB=∠B.
∵AB是⊙O的直径,∴∠ACB=90°,∴∠CAB+∠B=90°,∴3∠B=90° ,∴∠B=30°;
(3)由(2)知,∠DAB=30°.又∵∠DOB=2∠DAB,∴∠EOB=60°,∴∠OEB=90°.
在Rt△OEB中,∵OB=4,∠OBE=30°,∴OE=2,BE=![]() ,∴S=
,∴S=![]() =
=![]() =
=![]() .
.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
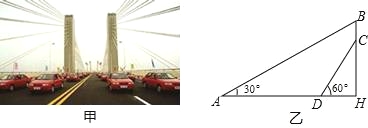
【题目】芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,正方形ABCD中,对角线AC和BD相交于点O.E、F分别是边AD、CD上的点,若AE=4cm,CF=3cm,且OE⊥OF,则EF的长为cm. 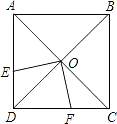
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:回答问题: ① ![]() =1+
=1+ ![]() ﹣
﹣ ![]() =1
=1 ![]()
② ![]() =1+
=1+ ![]() ﹣
﹣ ![]() =1
=1 ![]()
③ ![]() =1+
=1+ ![]() ﹣
﹣ ![]() =1
=1 ![]() ,…
,…
(1)根据上面三个等式的信息,猜想 ![]() =;
=;
(2)请按照上式反应的规律,试写出用n表示的等式;
(3)验证你的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 (聊城)下列说法中不正确的是( )
A. 抛掷一枚硬币,硬币落地时正面朝上是随机事件
B. 把4个球放入三个抽屉中,其中一个抽屉中至少有2个球是必然事件
C. 任意打开七年级下册数学教科书,正好是97页是确定事件
D. 一个盒子中有白球m个,红球6个,黑球n个(每个除了颜色外都相同).如果从中任取一个球,取得的是红球的概率与不是红球的概率相同,那么m与n的和是6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对抛物线y=x2+2x3而言,下列结论正确的是( )
A.与x轴有两个交点B.顶点坐标是(1,2)
C.与y轴的交点坐标是(0,3)D.开口向上
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com