
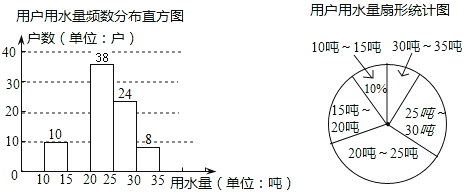
【题目】某市为提倡节约用水,准备实行自来水阶梯计算方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为了更好地决策,自来水公司随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图,(每组数据包括在右端点但不包括左端点),请你根据统计图解答下列问题:
(1)此次抽样调查的样本容量是___________
(2)补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区10万用户中约有多少用户的用水全部享受基本价格?
【答案】(1)100 (2)见解析,72° (3)6.8万
【解析】
(1)根据统计图可知“10吨~15吨的用户为10户,占到总数的10%”,从而可求得此次调查的总数.(2)先利用总数求得“15吨~20吨”的用户数,再用360°乘以它所占的百分比即可求得“15吨~20吨”部分的圆心角的度数.(3)用10万户乘以样本中用水量小于25吨的用户所占的比即可.
解:(1)此次调查的总数为:10÷10%=100(户),
∴此次抽样调查的样本容量是100.
(2)用水量在“15吨~20吨”的用户数为:100-10-38-24-8=20(户),
补全频数分布直方图如下:
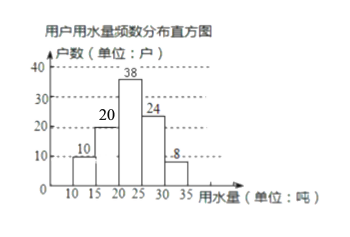
扇形图中“15吨~20吨”部分的圆心角的度数为:360°×![]() =72°,
=72°,
(3)少于25吨的用户数为: ![]() =6.8(万户)
=6.8(万户)
答:该地区10万用户中约有6.8万用户享受基本价格.


科目:初中数学 来源: 题型:
【题目】已知直线l1:y=![]() x-3与x轴,y轴分别交于点A和点B.
x-3与x轴,y轴分别交于点A和点B.
(1)求点A和点B的坐标;
(2)将直线l1向上平移6个单位后得到直线l2,求直线l2的函数解析式;
(3)设直线l2与x轴的交点为M,则△MAB的面积是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将分别标有数字1,2,3的三张卡片洗匀后,背面朝上放在桌面上.
(1)随机地抽取一张,求P(奇数);
(2)随机地抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字,能组成哪些两位数?恰好是“32”的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将长为20cm,宽为8cm的长方形白纸,按如图所示的方式粘合起来,粘合部分的宽为3cm.
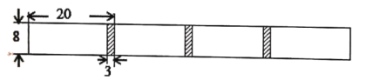
(1)根据题意,将下面的表格补充完整.
白纸张数x(张) | 1 | 2 | 3 | 4 | 5 | … |
纸条总长度y(cm) | 20 | 54 | 71 | … |
(2)直接写出y与x的关系式.
(3)要使粘合后的长方形总面积为1656cm2,则需用多少张这样的白纸?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线和直线l在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=﹣1,P1(x1,y1)、P2(x2,y2)是抛物线上的点,P3(x3,y3)是直线l上的点,且﹣1<x1<x2,x3<﹣1,则y1、y2、y3的大小关系为( )

A. y1<y2<y3 B. y3<y1<y2 C. y3<y2<y1 D. y2<y1<y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)甲、乙、丙、丁四人做传球游戏:第一次由甲将球随机传给乙、丙、丁中的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人中的某一人.求第二次传球后球回到甲手里的概率.(请用“画树状图”的方式给出分析过程)
(2)如果甲跟另外n(n≥2)个人做(1)中同样的游戏,那么,第三次传球后球回到甲手里的概率是 (请直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,根据图中信息解答下列问题:
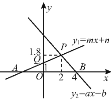
(1)关于x的不等式ax+b>0的解集是 .
(2)关于x的不等式mx+n<1的解集是 .
(3)当x为何值时,y1≤y2?
(4)当x为何值时,0<y2<y1?
查看答案和解析>>
科目:初中数学 来源: 题型:
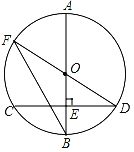
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点F在⊙O上,FD恰好经过圆心O,连接FB.
(1)若∠F=∠D,求∠F的度数;
(2)若CD=24,BE=8,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形DEF是三角形ABC经过某种变换得到的图形,点A与点D、点B与点E、点C与点F分别是对应点.观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D、点B与点E、点C与点F的坐标,并说出三角形DEF是由三角形ABC经过怎样的变换得到的;
(2)若点Q(a+3,4-b)是点P(2a,2b-3)通过上述变换得到的,求a-b的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com