
【题目】将长为20cm,宽为8cm的长方形白纸,按如图所示的方式粘合起来,粘合部分的宽为3cm.
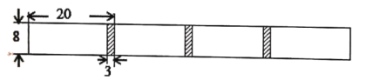
(1)根据题意,将下面的表格补充完整.
白纸张数x(张) | 1 | 2 | 3 | 4 | 5 | … |
纸条总长度y(cm) | 20 | 54 | 71 | … |
(2)直接写出y与x的关系式.
(3)要使粘合后的长方形总面积为1656cm2,则需用多少张这样的白纸?
【答案】(1)图形见解析(2)y=17x+3(3)12
【解析】
(1)根据纸条的长度变化,可得到答案;
(2)根据纸条的长度变化,可得到答案;
(3)根据面积和宽得到纸条的长,再由自变量与函数值的对应关系,可得答案.
(1) 当x=2时,y=20+17=2×17+3=37,
当x=5时,y=5×17+3=88,
故答案为:37,88;
根据题意,完成表格如下:
白纸张数x(张) | 1 | 2 | 3 | 4 | 5 | … |
纸条总长度y(cm) | 20 | 37 | 54 | 71 | 88 | … |
(2)由题意知y与x的关系式为y=17x+3,
故答案为:y=17x+3.
(3)1656÷8=207(cm)
当y=207时,17x+3=207,
解得:x=12,
所以,需要12张这样的白纸.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】如图,图1中ΔABC是等边三角形,DE是中位线,F是线段BC延长线上一点,且CF=AE,连接BE,EF.
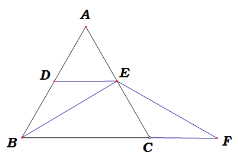

图1 图2
(1)求证:BE=EF;
(2)若将DE从中位线的位置向上平移,使点D、E分别在线段AB、AC上(点E与点A不重合),其他条件不变,如图2,则(1)题中的结论是否成立?若成立,请证明;若不成立.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位长度得到点A,过点A作y轴的平行线交反比例函数![]() 的图象于点B,AB=
的图象于点B,AB=![]() .
.
(1)求反比例函数的解析式;
(2)若P(![]() ,
, ![]() )、Q(
)、Q(![]() ,
, ![]() )是该反比例函数图象上的两点,且
)是该反比例函数图象上的两点,且![]() 时,
时, ![]() ,指出点P、Q各位于哪个象限?并简要说明理由.
,指出点P、Q各位于哪个象限?并简要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,2×2网格(每个小正方形的边长为1)中有A,B,C,D,E,F,G,H,O九个格点.抛物线l的解析式为y=(-1)nx2+bx+c(n为整数).

(1)n为奇数,且l经过点H(0,1)和C(2,1),求b,c的值,并直接写出哪个格点是该抛物线上的顶点;
(2)n为偶数,且l经过点A(1, 0)和B(2,0),通过计算说明点F(0,2)和H(0,1)是否在抛物线上;
(3)若l经过这九个格点中的三个,直接写出满足这样条件的抛物线条数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF.给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD=![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )
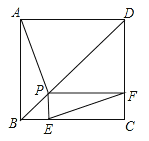
A. ①②③④ B. ①②④⑤ C. ②③④⑤ D. ①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以2cm/s的速度运动.如果点E、F同时出发,设运动时间为t(s)当t=______s时,以A、C、E、F为顶点四边形是平行四边形.
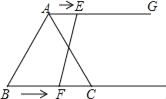
查看答案和解析>>
科目:初中数学 来源: 题型:
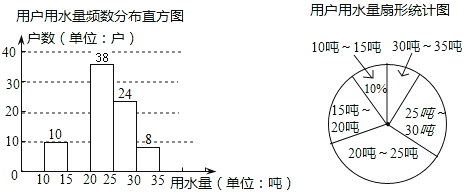
【题目】某市为提倡节约用水,准备实行自来水阶梯计算方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为了更好地决策,自来水公司随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图,(每组数据包括在右端点但不包括左端点),请你根据统计图解答下列问题:
(1)此次抽样调查的样本容量是___________
(2)补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区10万用户中约有多少用户的用水全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
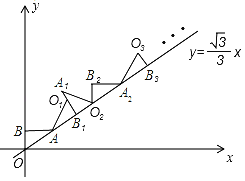
【题目】如图,点B的坐标是(0,1),AB⊥y轴,垂足为B,点A在直线y=![]() x,将△ABO绕点A顺时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=
x,将△ABO绕点A顺时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=![]() x上,再将△AB1O1绕点B1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=
x上,再将△AB1O1绕点B1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=![]() x上,依次进行下去…,则点O100的纵坐标是_____.
x上,依次进行下去…,则点O100的纵坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣2x+m﹣1=0有两个实数根.
(1)求m的取值范围;
(2)设p是方程的一个实数根,且满足(p2﹣2p+3)(m+4)=7,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com