
【题目】(1)已知函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的一个交点为A
的图象的一个交点为A![]() ,则
,则![]() = ________.
= ________.
(2)如果![]() 满足
满足![]() ,试求代数式
,试求代数式![]() 的值.
的值.
(3)已知![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)5;(3)-5.
;(2)5;(3)-5.
【解析】
(1)把点A(a,b)代入两个函数的解析式可得:b-a=5,ab=-2,将![]() 化简为
化简为![]() ,然后代值计算即可;
,然后代值计算即可;
(2)由题题意可知:![]() ,因此由
,因此由![]() 可得:
可得:![]() ,由此可得
,由此可得![]() ,这样由
,这样由![]() 即可求得所求的值了;
即可求得所求的值了;
(3)将![]() 的值化简,再将化简的结果代入
的值化简,再将化简的结果代入![]() 中计算即可.
中计算即可.
(1)∵函数y=x+5的图象与反比例函数y=-![]() 的图象的一个交点为A(a,b),
的图象的一个交点为A(a,b),
∴b=a+5,ab=-2,
∴b-a=5,
∴![]() ;
;
故答案为:![]() ;
;
(2)∵x2-3x+1=0,x≠0
∴x-3+![]() =0,
=0,
∴x+![]() =3,
=3,
∴(x-![]() )2=(x+
)2=(x+![]() )2-4=32-4=5;
)2-4=32-4=5;
(3)∵a=![]() =-2-
=-2-![]() ,b=
,b=![]() =-2+
=-2+![]() ,
,
∴a+b+ab
=-2-![]() -2+
-2+![]() +(-2-
+(-2-![]() )(-2+
)(-2+![]() )
)
=-4+(-1)
=-5.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶
点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图(3),
则三角板的最大边的长为( )
A. ![]() B.
B. ![]() C.
C.![]()
![]() D.
D. ![]()
![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学每天中午总是在规定时间打开学校大门,七年级同学小明每天中午同一时间从家骑自行车到学校,星期一中午他以每小时15千米的速度到校,结果在校门口等了6分钟才开门,星期二中午他以每小时9千米的速度到校,结果校门已开了6分钟,星期三中午小明想准时到达学校门口,那么小明骑自行车的速度应该为每小时多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=4,BC=5,∠ABC=60°,平行四边形ABCD的对角线AC、BD交于点O,过点O作OE⊥AD,则OE= . 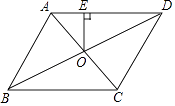
查看答案和解析>>
科目:初中数学 来源: 题型:
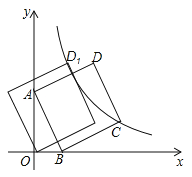
【题目】如图,直线![]() 与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线
与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线![]() (
(![]() )上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线
)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线![]() (
(![]() )上的点D1处,则a= .
)上的点D1处,则a= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE⊥DF,交AB于E,交BC于F,若S四边形BFDE=9,则AB的长为:
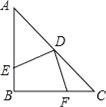
A. 3 B. 6 C. 9 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料: 小腾遇到这样一个问题:如图1,在△ABC中,点D在线段BC上,∠BAD=75°,∠CAD=30°,AD=2,BD=2DC,求AC的长.
小腾发现,过点C作CE∥AB,交AD的延长线于点E,通过构造△ACE,经过推理和计算能够使问题得到解决(如图 2).
请回答:求∠ACE的度数,AC的长.
参考小腾思考问题的方法,解决问题:
如图 3,在四边形 ABCD中,∠BAC=90°,∠CAD=30°,∠ADC=75°,AC与BD交于点E,AE=2,BE=2ED,求BC的长.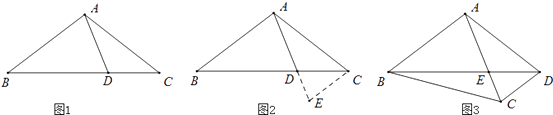
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点A(a,0),B(0,b),且a、b满足![]() =0, □ABCD的边AD与y轴交于点E(0,2),且E为AD中点,双曲线
=0, □ABCD的边AD与y轴交于点E(0,2),且E为AD中点,双曲线![]() 经过C、D两点.
经过C、D两点.
(1)求k的值;
(2)点P在双曲线![]() 上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
(3)以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,当T在AF上运动时,![]() 的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.
的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com