
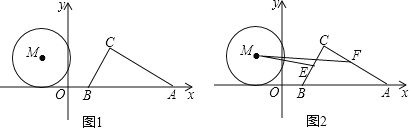
【题目】如图1,有一块直角三角板,其中![]() ,
,![]() ,
,![]() ,A、B在x轴上,点A的坐标为
,A、B在x轴上,点A的坐标为![]() ,圆M的半径为
,圆M的半径为![]() ,圆心M的坐标为
,圆心M的坐标为![]() ,圆M以每秒1个单位长度的速度沿x轴向右做平移运动,运动时间为t秒;
,圆M以每秒1个单位长度的速度沿x轴向右做平移运动,运动时间为t秒;
![]() 求点C的坐标;
求点C的坐标;
![]() 当点M在
当点M在![]() 的内部且
的内部且![]() 与直线BC相切时,求t的值;
与直线BC相切时,求t的值;
![]() 如图2,点E、F分别是BC、AC的中点,连接EM、FM,在运动过程中,是否存在某一时刻,使
如图2,点E、F分别是BC、AC的中点,连接EM、FM,在运动过程中,是否存在某一时刻,使![]() ?若存在,直接写出t的值,若不存在,请说明理由.
?若存在,直接写出t的值,若不存在,请说明理由.
【答案】(1)![]() ;(2)t=18s;(3)
;(2)t=18s;(3)![]() .
.
【解析】
(1)如图1中,作CH⊥AB于H.解直角三角形求出CH,OH即可.
(2)如图1﹣1中,设⊙M与直线BC相切于点N,作MH⊥AB于H.求出OH的长即可解决问题.
(3)设M(﹣5+t,3![]() ),EF
),EF![]() AB=8,由∠EMF=90°,可得EM2+MF2=EF2,由此构建方程即可解决问题.
AB=8,由∠EMF=90°,可得EM2+MF2=EF2,由此构建方程即可解决问题.
(1)如图1中,作CH⊥AB于H.
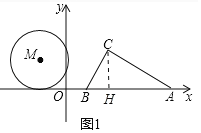
∵A(20,0),AB=16,∴OA=20,OB=4.在Rt△ABC中,∵∠ACB=90°,AB=16,∠CAB=30°,∴BC![]() AB=8,CH=BCsin60°=4
AB=8,CH=BCsin60°=4![]() ,BH=BCcos60°=4,∴OH=8,∴C(8,4
,BH=BCcos60°=4,∴OH=8,∴C(8,4![]() ).
).
(2)如图1﹣1中,设⊙M与直线BC相切于点N,作MH⊥AB于H.
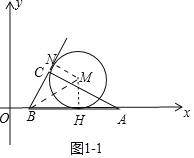
∵MN=MH=3![]() ,MN⊥BC,MH⊥BA,∴∠MBH=∠MBN=30°,∴BH
,MN⊥BC,MH⊥BA,∴∠MBH=∠MBN=30°,∴BH![]() MH=9,∴点M的运动路径的长为5+4+9=18,∴当点M在∠ABC的内部且⊙M与直线BC相切时,t的值为18s.
MH=9,∴点M的运动路径的长为5+4+9=18,∴当点M在∠ABC的内部且⊙M与直线BC相切时,t的值为18s.
(3)∵C(8,4![]() ),B(4,0),A(20,0).
),B(4,0),A(20,0).
∵CE=EB,CF=FA,∴E(6,2![]() ),F(14,2
),F(14,2![]() ),设M(﹣5+t,3
),设M(﹣5+t,3![]() ),EF
),EF![]() AB=8.
AB=8.
∵∠EMF=90°,∴EM2+MF2=EF2,∴(6+5﹣t)2+(![]() )2+(14+5﹣t)2+(
)2+(14+5﹣t)2+(![]() )2=82,整理得:t2﹣30t+212=0,解得:t=15±
)2=82,整理得:t2﹣30t+212=0,解得:t=15±![]() .
.


科目:初中数学 来源: 题型:
【题目】根据扬州市某风景区的旅游信息,![]() 公司组织一批员工到该风景区旅游,支付给旅行社
公司组织一批员工到该风景区旅游,支付给旅行社![]() 元.
元. ![]() 公司参加这次旅游的员工有多少人?
公司参加这次旅游的员工有多少人?
扬州市某风景区旅游信息表
旅游人数 | 收费标准 |
不超过 | 人均收费 |
超过 | 每增加 |
查看答案和解析>>
科目:初中数学 来源: 题型:
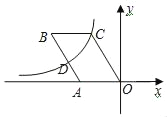
【题目】如图,ABCO的顶点B、C在第二象限,点A(﹣3,0),反比例函数y=![]() (k<0)图象经过点C和AB边的中点D,若∠B=α,则k的值为( )
(k<0)图象经过点C和AB边的中点D,若∠B=α,则k的值为( )
A. ﹣4tanαB. ﹣2sinαC. ﹣4cosαD. ﹣2tan
查看答案和解析>>
科目:初中数学 来源: 题型:
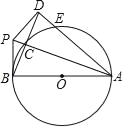
【题目】如图,AB是⊙O的直径,点D是⊙O外一点,AB=AD,BD交⊙O于点C,AD交⊙O于点E,点P是AC的延长线上一点,连接PB、PD,且PD⊥AD
(1)判断PB与⊙O的位置关系,并说明理由;
(2)连接CE,若CE=3,AE=7,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
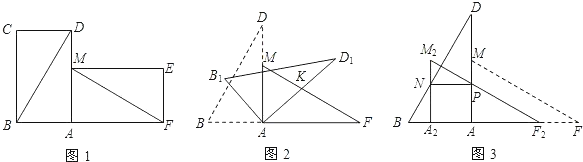
【题目】有两张完全重合的矩形纸片,小亮同学将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连接BD、MF,若此时他测得BD=8cm,∠ADB=30度.请回答下列问题:(1)试探究线段BD与线段MF的关系,并简要说明理由;
(2)小红同学用剪刀将△BCD与△MEF剪去,与小亮同学继续探究.他们将△ABD绕点A顺时针旋转得△AB1D1,AD1交FM于点K(如图2),设旋转角为β(0°<β<90°),当△AFK为等腰三角形时,请直接写出旋转角β的度数;
(3)若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=ax2(a≠0)与一次函数y=kx+b的图象相交于A(﹣1,﹣1),B(2,﹣4)两点,点P是抛物线上不与A,B重合的一个动点,点Q是y轴上的一个动点.
(1)请直接写出a,k,b的值及关于x的不等式ax2<kx﹣2的解集;
(2)当点P在直线AB上方时,请求出△PAB面积的最大值并求出此时点P的坐标;
(3)是否存在以P,Q,A,B为顶点的四边形是平行四边形?若存在,请直接写出P,Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在港口A的南偏东37°方向的海面上,有一巡逻艇B,A、B相距20海里,这时在巡逻艇的正北方向及港口A的北偏东67°方向上,有一渔船C发生故障.得知这一情况后,巡逻艇以25海里/小时的速度前往救援,问巡逻艇能否在1小时内到达渔船C处?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
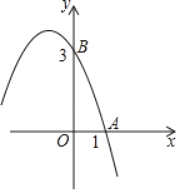
【题目】如图,已知抛物线y=﹣x2+bx+c的部分图象,A(1,0),B(0,3).
(1)求抛物线的解析式;
(2)若抛物线与x轴的另一个交点是C点,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com