
【题目】下列图形中,既是轴对称图形又是中心对称图形的是( )
A.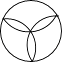
B.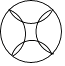
C.
D.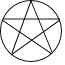
科目:初中数学 来源: 题型:
【题目】因为![]() ,所以
,所以![]() .这说明
.这说明![]() 能被
能被![]() 整除,同时也说明多项式
整除,同时也说明多项式![]() 有一个因式为
有一个因式为![]() ;另外,当
;另外,当![]() 多项式
多项式![]() 的值为
的值为![]() .阅读上述材料回答问题:
.阅读上述材料回答问题:
(1)由![]() 可知,当
可知,当![]() _时,多项式
_时,多项式![]() 的值为
的值为![]() ;
;
(2)一般地,如果一个关于字母![]() 的多项式
的多项式![]() 当
当![]() 时,
时,![]() 的值为
的值为![]() ,那么
,那么![]() 与代数式
与代数式![]() 之间有一定的关系,这种关系是:_____;
之间有一定的关系,这种关系是:_____;
(3)已知关于![]() 的多项式
的多项式![]() 能被
能被![]() 整除,试求
整除,试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD内接于⊙O,点E为AD上一点,连接AC,CB,∠B=∠AEC.
(1)如图1,求证:CE=CD;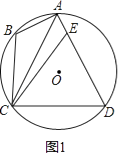
(2)如图2,若∠B+∠CAE=120°,∠ACD=2∠BAC,求∠BAD的度数;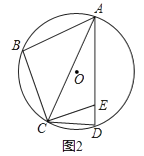
(3)如图3,在(2)的条件下,延长CE交⊙O于点G,若tan∠BAC= ![]() ,EG=2,求AE的长.
,EG=2,求AE的长.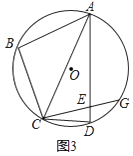
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2分别是7×6的网格,网格中的每个小正方形的边长均为1,点A、B在小正方形的顶点上.
(1)在图1中确定点C(点C在小正方形的顶点上),要求以A、B、C为顶点的三角形为锐角等腰三角形,画出此三角形(画出一个即可);
(2)在图2中确定点D(点D在小正方形的顶点上),要求以A、B、D为顶点的三角形是以AB为斜边的直角三角形,画出此三角形(画出一个即可),并直接写出此三角形的周长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江汉平原享有“中国小龙虾之乡”的美称,甲、乙两家农贸商店,平时以同样的价格出售品质相同的小龙虾,“龙虾节”期间,甲、乙两家商店都让利酬宾,付款金额y甲、y乙(单位:元)与原价x(单位:元)之间的函数关系如图所示:
(1)直接写出y甲,y乙关于x的函数关系式;
(2)“龙虾节”期间,如何选择甲、乙两家商店购买小龙虾更省钱?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABD,△ACE都是等边三角形,
(1)求证:△ABE≌△ADC;
(2)若∠ACD=15°,求∠AEB的度数;
(3)如图2,当△ABD与△ACE的位置发生变化,使C、E、D三点在一条直线上,求证:AC∥BE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC为等边三角形,点D为直线BC上一动点(点D不与点B,点C重合)。以AD为边作等边三角形ADE,连接CE。

(1)如图(1),当点D在边BC上时。
①求证:△ABD≌△ACE;
②直接判断结论BC=DC+CE是否成立(不需证明);
(2)如图2,当点D在边BC的延长线上时,其他条件不变,请写出BC,DC,CE之间存在的数量关系,并写出证明过程。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对任意一个两位数a,如果a满足个位数字与十位数字互不相同,且都不为零,那么称这个两位数为“迥异数”.将一个“迥异数”的个位数字与十位数字对调后得到一个新的两位数,把这个新两位数与原两位数的和与11的商记为f(a).例如:a=12,对调个位数字与十位数字得到新两位数21,新两位数与原两位数的和为21+12=33,和与11的商为3311=3,所以f(12)=3.
根据以上定义,回答下列问题:
(1)填空:
①下列两位数:40,42,44中,“迥异数”为 ;
②计算:f(23)= .
(2)如果一个“迥异数”b的十位数字是k,个位数字是2(k+1),且f(b)=11,请求出“迥异数”b.
(3)如果一个“迥异数”c,满足c5f(c)30,请直接写出满足条件的c的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com