
【题目】定义:对任意一个两位数a,如果a满足个位数字与十位数字互不相同,且都不为零,那么称这个两位数为“迥异数”.将一个“迥异数”的个位数字与十位数字对调后得到一个新的两位数,把这个新两位数与原两位数的和与11的商记为f(a).例如:a=12,对调个位数字与十位数字得到新两位数21,新两位数与原两位数的和为21+12=33,和与11的商为3311=3,所以f(12)=3.
根据以上定义,回答下列问题:
(1)填空:
①下列两位数:40,42,44中,“迥异数”为 ;
②计算:f(23)= .
(2)如果一个“迥异数”b的十位数字是k,个位数字是2(k+1),且f(b)=11,请求出“迥异数”b.
(3)如果一个“迥异数”c,满足c5f(c)30,请直接写出满足条件的c的值.
【答案】(1)①42,②5;(2)38;(3) 71或81或82或91或92或93.
【解析】
(1)①由“迥异数”的定义求解即可;
②根据定义计算可得;
(2)先将这个“迥异数”用k的代数式表示为:12k+2,再计算f(b)的值,最后利用等式f(b)=11即可求得b.
(3)设这个“迥异数”的十位和个位分别是m和n,将这个数c及f(c)分别用m和n的代数式表示,然后再通过给出的不等式求解即可.
解:(1)①由定义“个位数字与十位数字互不相同,且都不为零,那么称这个两位数为迥异数”可知,40,42,44中,“迥异数”为42.
故答案为:42.
②f(23)=(23+32)÷11=5.
故答案为:5.
(2)∵这个“迥异数”b的十位数字是k,个位数字是2(k+1)
∴b=10×k+2(k+1)=12k+2.
将这个数的个位和十位调换后为:10×2(k+1)+k=21k+20
∴f(b)=(12k+2+21k+20)÷11=3k+2
又f(b)=11
∴3k+2=11
∴k=3
故这个“迥异数”b=12k+2=38.
故答案为:38.
(3) 设这个“迥异数”c的个位为n,十位为m,则m≠n,且m,n均为大于1小于10的正整数.
则c=10m+n,调换个位和十位后为:10n+m
故f(c)=(10m+n+10n+m)÷11=m+n
∵c5f(c)30
∴10m+n-5(m+n) 30
整理得:5m-4n>30
∴![]() ,即
,即![]() ……①
……①
又∵![]()
∴![]() ,解得:
,解得:![]()
又n为正整数
故n=1或2或3
当n=1时,代入①中,m=7或8或9,此时c=71或81或91;
当n=2时,代入①中,m=8或9,此时c=82或92;
当n=3时,代入①中,m=9,此时c=93.
故所有满足条件的c有:71或81或82或91或92或93.


科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为 . 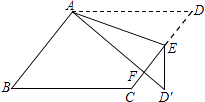
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b-2).

(1)直接写出点C1的坐标;
(2)在图中画出△A1B1C1;
(3)求△AOA1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】六一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.
(1)求A、B两种品牌服装每套进价分别为多少元?
(2)该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形A′B′C′是三角形ABC经过某种变换后得到的图形.
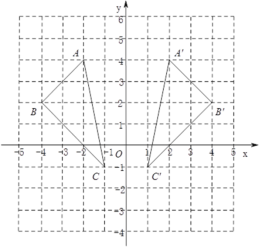
(1)分别写出点A和点A′,点B和点B′,点C和点C′的坐标;
(2)观察点A和点A′,点B和点B′,点C和点C′的坐标,用文字语言描述它们的坐标之间的关系 ;
(3)三角形ABC内任意一点M的坐标为(x,y),点M经过这种变换后得到点M′,则点M′的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
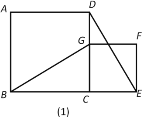
【题目】如图(1),正方形ABCD和正方形CEFG有一公共点C,且B,C,E在同一直线,连接BG,DE.
(1)请你猜想BG,DE的位置关系和数量关系,并说明理由.
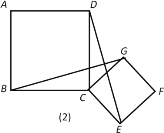
(2)若正方形CEFG绕点C按顺时针方向旋转一个角度后,如图(2),BG和DE是否还存在上述关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com