
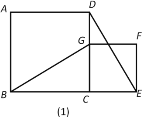
【题目】如图(1),正方形ABCD和正方形CEFG有一公共点C,且B,C,E在同一直线,连接BG,DE.
(1)请你猜想BG,DE的位置关系和数量关系,并说明理由.
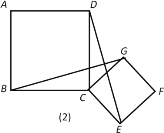
(2)若正方形CEFG绕点C按顺时针方向旋转一个角度后,如图(2),BG和DE是否还存在上述关系,并说明理由.
【答案】(1)BG⊥DE,BG=DE;(2)BG与DE仍具有上述关系,即BG⊥DE,BG=DE
【解析】
(1)由四边形ABCD,CEFG都是正方形,得到CB=CD,CG=CE,∠BCG=∠DCE=90°,于是Rt△BCG≌Rt△DCE,得到BG=DE,∠CBG=∠CDE,根据三角形内角和定理可得到∠DHG=∠GCB=90°,即BG⊥DE.
(2)BG和DE还有上述关系.证明的方法与(1)一样.
解:(1)BG⊥DE,BG=DE
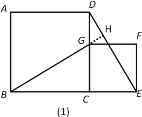
理由:如图(1),延长BG交DE于点H
∵四边形ABCD,CEFG都是正方形,
∴CB=CD,CG=CE,∠BCG=∠DCE=90°,
∴Rt△BCG≌Rt△DCE,
∴BG=DE,∠CBG=∠CDE,
而∠BGC=∠DGH,
∴∠DHG=∠GCB=90°,
即BG⊥DE.
∴BG=DE,BG⊥DE;
(2)BG与DE仍具有上述关系,即BG⊥DE,BG=DE
理由:如图(2),设BG与DC交于点M,与DE交于点H.
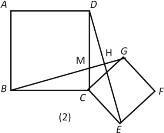
与(1)一样可证明△BCG≌△DCE,
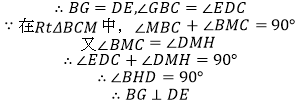


科目:初中数学 来源: 题型:
【题目】定义:对任意一个两位数a,如果a满足个位数字与十位数字互不相同,且都不为零,那么称这个两位数为“迥异数”.将一个“迥异数”的个位数字与十位数字对调后得到一个新的两位数,把这个新两位数与原两位数的和与11的商记为f(a).例如:a=12,对调个位数字与十位数字得到新两位数21,新两位数与原两位数的和为21+12=33,和与11的商为3311=3,所以f(12)=3.
根据以上定义,回答下列问题:
(1)填空:
①下列两位数:40,42,44中,“迥异数”为 ;
②计算:f(23)= .
(2)如果一个“迥异数”b的十位数字是k,个位数字是2(k+1),且f(b)=11,请求出“迥异数”b.
(3)如果一个“迥异数”c,满足c5f(c)30,请直接写出满足条件的c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知OB,OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD.
(1)若∠BOC=25°,∠MOB=15°,∠NOD=10°,求∠AOD的大小;
(2)若∠AOD=75°,∠MON=55°,求∠BOC的大小;
(3)若∠AOD=α,∠MON=β,求∠BOC的大小(用含α,β的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC的三边长分别为a,b,c,下列条件:①∠A=∠B-∠C;②∠A:∠B:∠C=3:4:5;③a2=(b+c)(b-c);④a:b:c=5:12:13,其中能判断△ABC是直角三角形的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
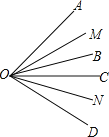
【题目】如图,平行四边形ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为( )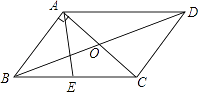
A.3cm
B.4cm
C.5cm
D.8cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由;
(2)若CE=8,CF=6,求OC的长
(3)连结AE,AF,当点O运动到何处时,四边形AECF是矩形?并说出你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com