
【题目】四边形ABCD内接于⊙O,点E为AD上一点,连接AC,CB,∠B=∠AEC.
(1)如图1,求证:CE=CD;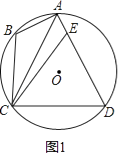
(2)如图2,若∠B+∠CAE=120°,∠ACD=2∠BAC,求∠BAD的度数;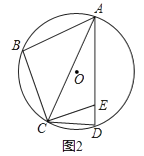
(3)如图3,在(2)的条件下,延长CE交⊙O于点G,若tan∠BAC= ![]() ,EG=2,求AE的长.
,EG=2,求AE的长.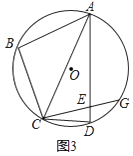
【答案】
(1)解:证明:∵四边形ABCD内接于⊙O
∴∠B+∠D=180°,
∵∠B=∠AEC,
∴∠AEC+∠D=180°,
∵∠AEC+∠CED=180°,
∴∠D=∠CED,
∴CE=CD.
(2)解:作CH⊥DE于H.
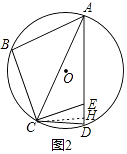
设∠ECH=α,由(1)CE=CD,
∴∠ECD=2α,
∵∠B=∠AEC,∠B+∠CAE=120°,
∴∠CAE+∠AEC=120°
∴∠ACE=180°﹣∠AEC﹣∠ACE=60°,
∴∠CAE=90°﹣∠ACH=90°﹣(60°+α)=30°﹣α,
∠ACD=∠ACH+∠HCD=60°+2α,
∵∠ACD=2∠BAC,
∴∠BAC=30°+α,
∴∠BAD=∠BAC+∠CAE=30°+α+30°﹣α=60°.
(3)解:连接AG,作GN⊥AC,AM⊥EG
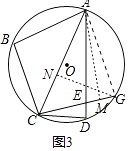
∵∠CED=∠AEG,∠CDE=∠AGE,∠CED=∠CDE,
∴∠AEG=∠AGE,
∴AE=AG,
∴EM=MG= ![]() EG=1,
EG=1,
∴∠EAG=∠ECD=2α,
∴∠CAG=∠CAD+∠DAG=30°﹣α+2α=∠BAC,
∵tan∠BAC= ![]() ,
,
∴设NG=5 ![]() m,可得AN=11m,AG=
m,可得AN=11m,AG= ![]() =14m,
=14m,
∵∠ACG=60°,
∴CN=5m,AM=8 ![]() m,MG=
m,MG= ![]() =2m=1,
=2m=1,
∴m= ![]() ,
,
∴CE=CD=CG﹣EG=10m﹣2=3
∴AE= ![]() =
= ![]() =7.
=7.
【解析】(1)根据圆内接四边形对角互补及平角的定义,得出∠B与∠D互补,∠AEC与∠CED互补,再根据等角的补角相等,得出∠D=∠CED,即可得出结论。
(2)作CH⊥DE于H.设∠ECH=α,先用含α的代数式分别表示出∠CAE和∠BAC,即可求得∠BAD的度数。
(3)连接AG,作GN⊥AC,AM⊥EG,先证明∠CAG=∠BAC,根据tan∠BAC的值,用含m的代数式分别表示出NG、AN、AG的长,再由∠ACG=60°,求出m的值,再根据勾股定理即可求得AE的长。
【考点精析】利用勾股定理的概念和圆内接四边形的性质对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】抛物线y=x2﹣2mx﹣3m2(m>0)与x轴交于A、B两点,A点在B点左边,与y轴交于C点,顶点为M.
(1)当m=1时,求点A、B、M坐标;
(2)如图(1)的条件下,若P为抛物线上一个动点,以AP为斜边的等腰直角的直角顶点Q在对称轴上,(A、P、Q按顺时针方向排列),求P点坐标.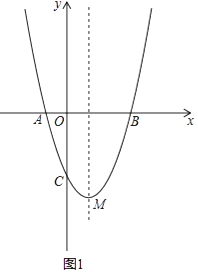
(3)如图2,若一次函数y=kx+b过B点且与抛物线只有一个公共点,平移直线y=kx+b,使其过抛物线的顶点M,与抛物线另一个交点为D,与x轴交于F点,当m变化时,求证:DF:MF是定值.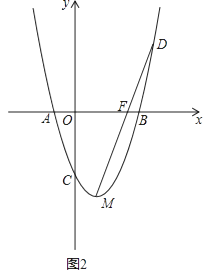
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,P为AD边上一点,沿直线BP将△ABP翻折至△EBP(点A的对应点为点E),PE与CD相交于点O,且OE=OD.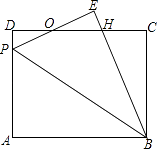
(1)求证:PE=DH;
(2)若AB=10,BC=8,求DP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 400 | 280 |
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆) | 载客量(人) | 租金(元) | |
A | x | 45x | 400x |
B | 5-x |
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小磊老师从甲地去往10千米的乙地,开始以一定的速度行驶,之后由于道路维修,速度变为原来的四分之一,过了维修道路后又变为原来的速度到达乙地.设小磊老师行驶的时间为x(分钟),行驶的路程为y(千米),图中的折线表示y与x之间的函数关系,则小磊老师从甲地到达乙地所用的时间是( )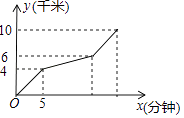
A.15分钟
B.20分钟
C.25分钟
D.30分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形A′B′C′是三角形ABC经过某种变换后得到的图形.
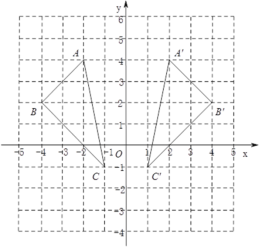
(1)分别写出点A和点A′,点B和点B′,点C和点C′的坐标;
(2)观察点A和点A′,点B和点B′,点C和点C′的坐标,用文字语言描述它们的坐标之间的关系 ;
(3)三角形ABC内任意一点M的坐标为(x,y),点M经过这种变换后得到点M′,则点M′的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com