
【题目】某商场销售一批名牌衬衫,平均每天可销售20件,每件盈利40元.为了扩大销售,增加盈利,尽量减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价5元,商场平均每天可多售出10件.求:
(1)若商场每件衬衫降价4元,则商场每天可盈利多少元?
(2)若商场平均每天要盈利1200元,每件衬衫应降价多少元?
(3)要使商场平均每天盈利1600元,可能吗?请说明理由.
【答案】(1)商场每件衬衫降价4元,则商场每天可盈利1008元;(2)每件衬衫应降价20元;
(3)不可能.理由见解析.
【解析】
(1)根据题意得到每天的销售量,然后由销售量×每件盈利进行解答;
(2)利用衬衣平均每天售出的件数×每件盈利=每天销售这种衬衣利润列出方程解答即可;
(3)同样列出方程,若方程有实数根则可以,否则不可以.
(1)![]() ×(40-4)=1008(元).
×(40-4)=1008(元).
答:商场每件衬衫降价4元,则商场每天可盈利1008元.
(2)设每件衬衫应降价x元,
根据题意,得(40-x)(20+2x)=1200,
整理,得x2-30x+200=0,
解得x1=10,x2=20,
∵要尽量减少库存,
∴x=20.
答:每件衬衫应降价20元.
(3)不可能.理由如下:
令(40-x)(20+2x)=1600,
整理得x2-30x+400=0,
∵Δ=900-4×400<0,
∴商场平均每天不可能盈利1600元.


科目:初中数学 来源: 题型:
【题目】某中学开展了“手机伴我行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成图①、图②不完整的统计图,已知问卷调查中“查资料”的人数是40人,条形统计图中“0~1表示每周使用手机的时间大于0小时而小于或等于1小时,以此类推.

(1)本次问卷调查一共调查了多少名学生?
(2)补全条形统计图;
(3)该校共有学生1200人,估计每周使用手机“玩游戏”是多少名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
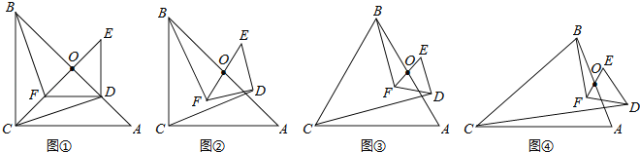
【题目】如图①,△ABC与△DEF都是等腰直角三角形,∠ACB=∠EDF=90°,且点D在AB边上,AB、EF的中点均为O,连结BF、CD、CO,显然点C、F、O在同一条直线上,可以证明△BOF≌△COD,则BF=CD.
解决问题
(1)将图①中的Rt△DEF绕点O旋转得到图②,猜想此时线段BF与CD的数量关系,并证明你的结论;
(2)如图③,若△ABC与△DEF都是等边三角形,AB、EF的中点均为O,上述(1)中的结论仍然成立吗?如果成立,请说明理由;如不成立,请求出BF与CD之间的数量关系;
(3)如图④,若△ABC与△DEF都是等腰三角形,AB、EF的中点均为0,且顶角∠ACB=∠EDF=α,请直接写出![]() 的值(用含α的式子表示出来)
的值(用含α的式子表示出来)
查看答案和解析>>
科目:初中数学 来源: 题型:
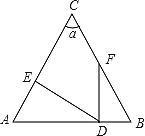
【题目】如图∠A=∠B,∠C=![]() ,DE⊥AC于点E,FD⊥AB于点D.
,DE⊥AC于点E,FD⊥AB于点D.
(1)若∠EDA=25°,则∠EDF=________°;
(2)若∠A=65°,则∠EDF=_______°;
(3)若![]() =50°,则∠EDF=_______°;
=50°,则∠EDF=_______°;
(4)若∠EDF=65°,则![]() _______°;
_______°;
(5)∠EDF与![]() 的关系为_______.
的关系为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 75 | 80 | 90 |
面试 | 93 | 70 | 68 |
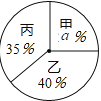
根据录用程序,学校组织200名学生采用投票推荐的方式,对三人进行民主测评,三人得票率(没有弃权,每位同学只能推荐1人)如扇形统计图所示,每得一票记1分.
(1)扇形统计图中![]() = , 分别计算三人民主评议的得分;
= , 分别计算三人民主评议的得分;
(2)根据实际需要,学校将笔试、面试、民主评议三项得分按4:3:3的比例确定个人成绩,得分最高者将被选中,通过计算说明三人中谁被选中?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(2,3),B(-3,n)两点.
的图象交于A(2,3),B(-3,n)两点.
(1)求一次函数和反比例函数的解析式;
(2)若P是y轴上一点,且满足△PAB的面积是5,求OP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某开发区计划在一块四边形的空地ABCD上种植草坪,已知∠A=90°,AB=4m,BC=12m,CD=13m,DA=3m,种植每平方米草皮的预算费用为300元,若第一年对草坪的保养费用占种植草皮总预算的4%,以后每年的保养费用都将在前一年的基础上递增2%,求第三年的草坪保养费用.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
![]() 根据图示填写下表:
根据图示填写下表:
平均数 | 中位数 | 众数 | |
A校 | ______ | 85 | ______ |
B校 | 85 | ______ | 100 |
![]() 结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
![]() 计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.

查看答案和解析>>
科目:初中数学 来源: 题型:
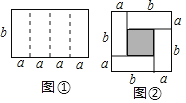
【题目】如图①是一个长为4a、宽为b的长方形,沿图中虚线用剪刀将其平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图②)
自主探索:
(1)仔细观察图形,完成下列问题
①图②中的阴影部分的面积为_____;
②观察图②,请你写出(a+b)2、(a-b)2、ab之间的等量关系是_____;
知识运用:
(2)若x-y=5,xy=![]() ,根据(1)中的结论,求(x+y)2的值;
,根据(1)中的结论,求(x+y)2的值;
知识延伸
(3)根据你探索发现的结论,完成下列问题:
设A=![]() ,B=x+2y-3
,B=x+2y-3
计算(A-B)2-(A+B)2的结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com