
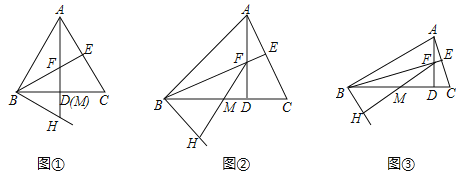
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌABЃНBCЃЌADЁЭBCгкЕуDЃЌBEЁЭACгкЕуEЃЌADгыBEНЛгкЕуFЃЌBHЁЭABгкЕуBЃЌЕуMЪЧBCЕФжаЕуЃЌСЌНгFMВЂбгГЄНЛBHгкЕуHЃЎ
ЃЈ1ЃЉдкЭМЂйжаЃЌЁЯABCЃН60ЁуЃЌAFЃН3ЪБЃЌFCЃНЁЁ ЁЁЃЌBHЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉдкЭМЂкжаЃЌЁЯABCЃН45ЁуЃЌAFЃН2ЪБЃЌFCЃНЁЁ ЁЁЃЌBHЃНЁЁ ЁЁЃЛ
ЃЈ3ЃЉДгЕкЃЈ1ЃЉЁЂЃЈ2ЃЉжаФуЗЂЯжСЫЪВУДЙцТЩЃПдкЭМЂлжаЃЌЁЯABCЃН30ЁуЃЌAFЃН1ЪБЃЌЪдВТЯыBHЕШгкЖрЩйЃПВЂжЄУїФуЕФВТЯыЃЎ
ЁОД№АИЁПЃЈ1ЃЉ3ЃЌ3ЃЛЃЈ2ЃЉ2ЃЌ2ЃЛЃЈ3ЃЉДгЕкЃЈ1ЃЉЁЂЃЈ2ЃЉжаЗЂЯжAFЃНCFЃНBHЃЌ BHЃН1ЃЌМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉШчЭМЂйСЌНгCFЃЌгЩДЙаФЕФаджЪПЩЕУCFЁЭABЃЌПЩЕУCFЁЮBHЃЌгЩЁАASAЁБПЩжЄЁїBMHЁеЁїCMFЃЌПЩЕУBHЃНCFЃЌгЩЯпЖЮДЙжБЦНЗжЯпЕФаджЪПЩЕУAFЃНCFЃЌПЩЕУAFЃНCFЃНBHЃН3ЃЛ
ЃЈ2ЃЉШчЭМЂкСЌНгCFЃЌгЩДЙаФЕФаджЪПЩЕУCFЁЭABЃЌПЩЕУCFЁЮBHЃЌгЩЁАASAЁБПЩжЄЁїBMHЁеЁїCMFЃЌПЩЕУBHЃНCFЃЌгЩЯпЖЮДЙжБЦНЗжЯпЕФаджЪПЩЕУAFЃНCFЃЌПЩЕУAFЃНCFЃНBHЃН2ЃЛ
ЃЈ3ЃЉШчЭМЂлСЌНгCFЃЌгЩДЙаФЕФаджЪПЩЕУCFЁЭABЃЌПЩЕУCFЁЮBHЃЌгЩЁАASAЁБПЩжЄЁїBMHЁеЁїCMFЃЌПЩЕУBHЃНCFЃЌгЩЯпЖЮДЙжБЦНЗжЯпЕФаджЪПЩЕУAFЃНCFЃЌПЩЕУAFЃНCFЃНBHЃН1ЃЎ
НтЃКЃЈ1ЃЉШчЭМЂйСЌНгCFЃЌ
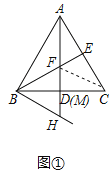
ЁпADЁЭBCЃЌBEЁЭACЃЌ
ЁрCFЁЭABЃЌ
ЁпBHЁЭABЃЌ
ЁрCFЁЮBHЃЌ
ЁрЁЯCBHЃНЁЯBCFЃЌ
ЁпЕуMЪЧBCЕФжаЕуЃЌ
ЁрBMЃНMCЃЌ
дкЁїBMHКЭЁїCMFжаЃЌ
 ЃЌ
ЃЌ
ЁрЁїBMHЁеЁїCMFЃЈASAЃЉЃЌ
ЁрBHЃНCFЃЌ
ЁпABЃНBCЃЌBEЁЭACЃЌ
ЁрBEДЙжБЦНЗжACЃЌ
ЁрAFЃНCFЃЌ
ЁрBHЃНAFЃЌ
ЁрAFЃНCFЃНBHЃН3ЃЌ
ЃЈ2ЃЉШчЭМЂкЃЌСЌНгCFЃЌ
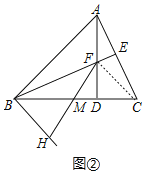
ЁпADЁЭBCЃЌBEЁЭACЃЌ
ЁрCFЁЭABЃЌ
ЁпBHЁЭABЃЌ
ЁрCFЁЮBHЃЌ
ЁрЁЯCBHЃНЁЯBCFЃЌ
ЁпЕуMЪЧBCЕФжаЕуЃЌ
ЁрBMЃНMCЃЌ
дкЁїBMHКЭЁїCMFжаЃЌ
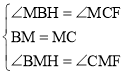
ЁрЁїBMHЁеЁїCMFЃЈASAЃЉЃЌ
ЁрBHЃНCFЃЌ
ЁпABЃНBCЃЌBEЁЭACЃЌ
ЁрBEДЙжБЦНЗжACЃЌ
ЁрAFЃНCFЃЌ
ЁрBHЃНAFЃЌ
ЁрAFЃНCFЃНBHЃН2ЃЌ
ЃЈ3ЃЉДгЕкЃЈ1ЃЉЁЂЃЈ2ЃЉжаЗЂЯжAFЃНCFЃНBHЃЛ
ВТЯыBHЃН1ЃЌ
РэгЩШчЯТЃК
ШчЭМЂлЃЌСЌНгCFЃЌ
ЁпADЁЭBCЃЌBEЁЭACЃЌ
ЁрCFЁЭABЃЌ
ЁпBHЁЭABЃЌ
ЁрCFЁЮBHЃЌ
ЁрЁЯCBHЃНЁЯBCFЃЌ
ЁпЕуMЪЧBCЕФжаЕуЃЌ
ЁрBMЃНMCЃЌ
дкЁїBMHКЭЁїCMFжаЃЌ
ЁрЁїBMHЁеЁїCMFЃЈASAЃЉЃЌ
ЁрBHЃНCFЃЌ
ЁпABЃНBCЃЌBEЁЭACЃЌ
ЁрBEДЙжБЦНЗжACЃЌ
ЁрAFЃНCFЃЌ
ЁрBHЃНAFЃЌ
ЁрAFЃНCFЃНBHЃН1ЃЎ


 УћХЦбЇаЃЗжВужмжмВтЯЕСаД№АИ
УћХЦбЇаЃЗжВужмжмВтЯЕСаД№АИ ЛЦИдКЃЕэШЋГЬХргХВтЪдОэЯЕСаД№АИ
ЛЦИдКЃЕэШЋГЬХргХВтЪдОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌADЁЭBCЃЌEFДЙжБЦНЗжACЃЌНЛACгкЕуFЃЌНЛBCгкЕуEЃЌЧвBD=DEЃЎ
ЂХШєЁЯBAE=40ЁуЃЌЧѓЁЯCЕФЖШЪ§ЃЛ
ЂЦШєЁїABCжмГЄ13cmЃЌAC=6cmЃЌЧѓDCГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЇаЃМЦЛЎЮЊЁАЮвКЭЮвЕФзцЙњЁБбнНВБШШќЙКТђНБЦЗЃЎвбжЊЙКТђ3ИіAНБЦЗКЭ2ИіBНБЦЗЙВаш120дЊЃЛЙКТђ5ИіAНБЦЗКЭ4ИіBНБЦЗЙВаш210дЊЃЎ
ЃЈ1ЃЉЧѓAЃЌBСНжжНБЦЗЕФЕЅМлЃЛ
ЃЈ2ЃЉбЇаЃзМБИЙКТђAЃЌBСНжжНБЦЗЙВ30ИіЃЌЧвAНБЦЗЕФЪ§СПВЛЩйгкBНБЦЗЪ§СПЕФ![]() ЃЎЧыЩшМЦГізюЪЁЧЎЕФЙКТђЗНАИЃЌВЂЫЕУїРэгЩЃЎ
ЃЎЧыЩшМЦГізюЪЁЧЎЕФЙКТђЗНАИЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
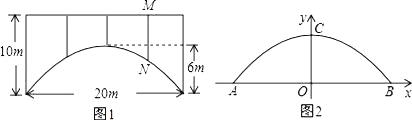
ЁОЬтФПЁПвЛзљЙАЧХЕФТжРЊЪЧХзЮяЯпаЭЃЈШчЭМ1ЫљЪОЃЉЃЌЙАИп6mЃЌПчЖШ20mЃЌЯрСкСНжЇжљМфЕФОрРыОљЮЊ5mЃЎ
ЃЈ1ЃЉНЋХзЮяЯпЗХдкЫљИјЕФжБНЧзјБъЯЕжаЃЈШчЭМ2ЫљЪОЃЉЃЌЦфБэДяЪНЪЧy=ax2+cЕФаЮЪНЃЎЧыИљОнЫљИјЕФЪ§ОнЧѓГіaЃЌcЕФжЕЃЎ
ЃЈ2ЃЉЧѓжЇжљMNЕФГЄЖШЃЎ
ЃЈ3ЃЉЙАЧХЯТЕиЦНУцЪЧЫЋЯђааГЕЕРЃЈе§жаМфЪЧвЛЬѕПэ2mЕФИєРыДјЃЉЃЌЦфжаЕФвЛЬѕааГЕЕРФмЗёВЂХХааЪЛПэ2mЁЂИп3mЕФШ§СОЦћГЕЃЈЦћГЕМфЕФМфИєКіТдВЛМЦЃЉЃПЧыЫЕЫЕФуЕФРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌABЃНACЃЎOЪЧЁїABCФквЛЕуЃЌODЪЧABЕФДЙжБЦНЗжЯпЃЌOFЁЭACЃЌЧвODЃНOFЃЎ
ЃЈ1ЃЉЕБЁЯOACЃН27ЁуЪБЃЌЧѓЃКЁЯOBCЕФЖШЪ§ЃЎ
ЃЈ2ЃЉЧѓжЄЃКAFЃНCFЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпy=ax2+bx+cЃЈaЁй0ЃЉЕФЖдГЦжсЮЊжБЯпx=1ЃЌгыxжсЕФвЛИіНЛЕузјБъЮЊЃЈЉ1ЃЌ0ЃЉЃЌЦфВПЗжЭМЯѓШчЭМЫљЪОЃЎЯТСаНсТлЃКЂйЗНГЬ=ax2+bx+c=0ЕФСНИіИљЪЧx1=Љ1ЃЌx2=3ЃКЂкaЉb+c=0ЃЛЂл8a+cЃМ0ЃЛЂмЕБyЃО0ЪБЃЌxЕФШЁжЕЗЖЮЇЪЧЉ1ЃМxЃМ3ЃЛЂнЕБyЫцxЕФдіДѓЖјдіДѓЪБЃЌвЛЖЈгаxЃМOЃЎЦфжаНсТле§ШЗЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ
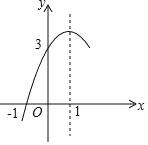
A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
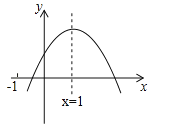
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§![]() ЕФЭМЯѓШчЭМЫљЪОЃЌгавдЯТНсТлЃК
ЕФЭМЯѓШчЭМЫљЪОЃЌгавдЯТНсТлЃК
ЂйabcЃО0ЃЌ
ЂкaЉb+cЃМ0ЃЌ
Ђл2a=bЃЌ
Ђм4a+2b+cЃО0ЃЌ
ЂнШєЕуЃЈЉ2ЃЌ![]() ЃЉКЭЃЈ
ЃЉКЭЃЈ![]() ЃЌ
ЃЌ![]() ЃЉдкИУЭМЯѓЩЯЃЌдђ
ЃЉдкИУЭМЯѓЩЯЃЌдђ![]() ЃЎ
ЃЎ
Цфжае§ШЗЕФНсТлЪЧ ЃЈЬюШые§ШЗНсТлЕФађКХЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
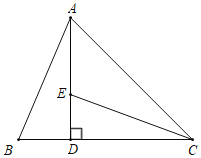
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯACBЃН45ЁуЃЌЙ§ЕуAзїADЁЭBCгкЕуDЃЌЕуEЮЊADЩЯвЛЕуЃЌЧвEDЃНBDЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїABDЁеЁїCEDЃЛ
ЃЈ2ЃЉШєCEЮЊЁЯACDЕФНЧЦНЗжЯпЃЌЧѓЁЯBACЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкФГаЃОйАьЕФ 2012 ФъЧяМОдЫЖЏЛсНсЪјжЎКѓЃЌбЇаЃашвЊЮЊВЮМгдЫЖЏЛсЕФЭЌбЇУЧЗЂМЭФюЦЗЃЎаЁЭѕИКд№ЕНФГЩЬГЁТђФГжжМЭФюЦЗЃЌИУЩЬГЁЙцЖЈЃКвЛДЮадЙКТђИУМЭФюЦЗ 200 ИівдЩЯПЩвдАДелПлМлГіЪлЃЛЙКТђ 200 ИівдЯТЃЈАќРЈ 200 ИіЃЉжЛФмАДдМлГіЪлЃЎаЁЭѕШєАДеедМЦЛЎЕФЪ§СПЙКТђМЭФюЦЗЃЌжЛФмАДдМлИЖПюЃЌЙВашвЊ 1050 дЊЃЛШєЖрТђ 35 ИіЃЌдђАДелПлМлИЖПюЃЌЧЁКУЙВаш 1050 дЊЃЎЩшаЁЭѕАДдМЦЛЎЙКТђМЭФюЦЗ x ИіЃЎ
ЃЈ1ЃЉЧѓ x ЕФЗЖЮЇЃЛ
ЃЈ2ЃЉШчЙћАДдМлЙКТђ 5 ИіМЭФюЦЗгыАДДђелМлЙКТђ 6 ИіМЭФюЦЗЕФЧЎЪ§ЯрЭЌЃЌФЧУДаЁЭѕдМЦЛЎЙКТђЖрЩйИіМЭФюЦЗЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com