
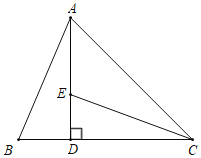
【题目】如图,在△ABC中,∠ACB=45°,过点A作AD⊥BC于点D,点E为AD上一点,且ED=BD.
(1)求证:△ABD≌△CED;
(2)若CE为∠ACD的角平分线,求∠BAC的度数.
【答案】(1)见解析;(2)∠BAC=67.5°.
【解析】
(1)证出△ADC是等腰直角三角形,得出AD=CD,∠CAD=∠ACD=45°,由SAS证明△ABD≌△CED即可;
(2)由角平分线定义得出∠ECD=![]() ∠ACD=22.5°,由全等三角形的性质得出∠BAD=∠ECD=22.5°,即可得出答案.
∠ACD=22.5°,由全等三角形的性质得出∠BAD=∠ECD=22.5°,即可得出答案.
解:(1)证明:∵AD⊥BC,∠ACB=45°,
∴∠ADB=∠CDE=90°,△ADC是等腰直角三角形,
∴AD=CD,∠CAD=∠ACD=45°,
在△ABD与△CED中,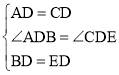 ,
,
∴△ABD≌△CED(SAS);
(2)解:∵CE为∠ACD的角平分线,
∴∠ECD=![]() ∠ACD=22.5°,
∠ACD=22.5°,
由(1)得:△ABD≌△CED,
∴∠BAD=∠ECD=22.5°,
∴∠BAC=∠BAD+∠CAD=22.5°+45°=67.5°.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】某天,小王去朋友家借书,在朋友家停留一段时间后,返回家中,如图是他离家的路程(千米)与时间(分)的关系的图象,根据图象信息,下列说法正确的是( )

A. 小王去时的速度大于回家的速度B. 小王在朋友家停留了10分钟
C. 小王去时所花时间少于回家所花时间D. 小王去时走上坡路施,回家时走下坡路
查看答案和解析>>
科目:初中数学 来源: 题型:
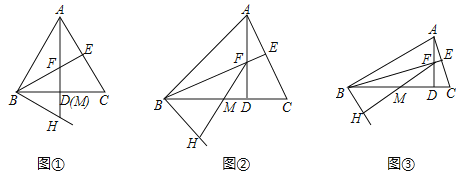
【题目】如图,在△ABC中,AB=BC,AD⊥BC于点D,BE⊥AC于点E,AD与BE交于点F,BH⊥AB于点B,点M是BC的中点,连接FM并延长交BH于点H.
(1)在图①中,∠ABC=60°,AF=3时,FC= ,BH= ;
(2)在图②中,∠ABC=45°,AF=2时,FC= ,BH= ;
(3)从第(1)、(2)中你发现了什么规律?在图③中,∠ABC=30°,AF=1时,试猜想BH等于多少?并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中AB=AC,△AED中AE=AD,∠EAD=∠BAC,AC与BD交于点O.
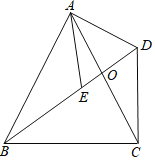
(1)试确定∠ADC与∠AEB间的数量关系,并说明理由;
(2)若∠ACB=65°,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
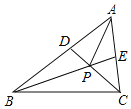
【题目】如图,任意画一个∠BAC=60°的△ABC,再分别作△ABC的两条角平分线BE和CD,BE和CD相交于点P,连接AP,有以下结论:①∠BPC=120°;②AP平分∠BAC;③AD=AE;④PD=PE;⑤BD+CE=BC;其中正确的结论为_____.(填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B,C三点在同一直线上,分别以AB,BC(AB>BC)为边,在直线AC的同侧作等边ΔABD和等边ΔBCE,连接AE交BD于点M,连接CD交BE于点N,连接MN. 以下结论:①AE=DC,②MN//AB,③BD⊥AE,④∠DPM=60°,⑤ΔBMN是等边三角形.其中正确的是__________(把所有正确的序号都填上).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等边△ABC中,点D,E分别在边AB,AC上,AD=AE,连接BE,CD,点M、N、P分别是BE、CD、BC的中点.
(1)观察猜想:图1中,△PMN的形状是 ;
(2)探究证明:把△ADE绕点A逆时针方向旋转到图2的位置,△PMN的形状是否发生改变?并说明理由;
(3)拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=1,AB=3,请直接写出△PMN的周长的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解,补全证明过程及推理依据.
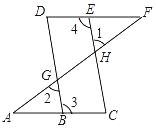
已知:如图,点E在直线DF上,点B在直线AC上,∠1=∠2,∠3=∠4.
求证∠A=∠F
证明:∵∠1=∠2(已知)
∠2=∠DGF( )
∴∠1=∠DGF(等量代换)
∴ ∥ ( )
∴∠3+∠ =180°( )
又∵∠3=∠4(已知)
∴∠4+∠C=180°(等量代换)
∴ ∥ ( )
∴∠A=∠F( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金堂某养鸭场有1800只鸭准备对外出售.从中随机抽取了一部分鸭,根据它们的质量(单位:![]() ),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:

(1)养鸭场随机共抽取鸭______只,并补全条形统计图;
(2)请写出统计的这组数据的众数为______、中位数为_______,并求这组数据的平均数(精确到0.01);
(3)根据样本数据,估计这1800只鸭中,质量为![]() 的约有多少只?
的约有多少只?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com