
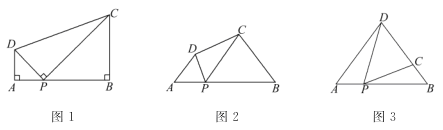
����Ŀ�� (1)�����⣺��ͼ1�����ı���ABCD�У���PΪAB��һ�㣬��DPC=��A=��B=90������֤��AD��BC=AP��BP��
(2)��̽������ͼ2�����ı���ABCD�У���PΪAB��һ�㣬����DPC=��A=��B=��ʱ�����������Ƿ���Ȼ������˵�����ɣ�
(3)��Ӧ�ã������ã�1����2����õľ��������⣺
��ͼ3������ABD�У�AB=6��AD=BD=5����P��ÿ��1����λ���ȵ��ٶȣ��ɵ�A �������ر�AB���B�˶�����������DPC=��A�����P���˶�ʱ��Ϊt���룩����DC�ij�����ABD�ױ��ϵĸ����ʱ����t��ֵ��
���𰸡�(1)��֤�����̼�������(2)��֤�����̼�������(3)��t=1���5��.
��������
���������(1)��������DPC=��A=��B=90���ó���ADP+��APD=��BPC+��APD=90��������ADP=��BPC���Ӷ��ó���ADP����BPC���ƣ��Ӷ��ó��𰸣�(2)������ͬ����֤�������ó����������ƣ��Ӷ��ó��𰸣�(3)������D��DE��AB�ڵ�E����AE=BE=3�����ݹ��ɶ����ó�DE=4����AP=t����BP=6��t������(1)(2)�Ķ����г�����t�ķ��̣��Ӷ����t��ֵ.
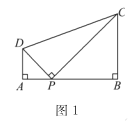
���������(1)����ͼ1 �ߡ�DPC=��A=��B=90�������ADP+��APD=90����
��BPC+��APD=90�������ADP =��BPC ���ADP�ס�BPC����![]() ��AD��BC=AP��BP��
��AD��BC=AP��BP��
(2)������AD��BC=AP��BP �Գ�����
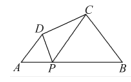
���ɣ���ͼ2���ߡ�BPD=��DPC+��BPC�� ���ߡ�BPD=��A+��ADP�����DPC+��BPC =��A+��ADP��
�ߡ�DPC =��A=�������BPC =��ADP ���ߡ�A=��B=�������ADP�ס�BPC����![]()
��AD��BC=AP��BP��
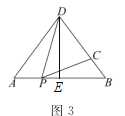
(3)����ͼ3������D��DE��AB�ڵ�E����AD=BD=5��AB=6�� ��AE=BE=3���ɹ��ɶ�����DE=4��
��DC=DE=4����BC=5-4=1������AD=BD�����A=��B������֪����DPC =��A�����DPC =��A=��B��
�ɣ�1������2���ɵã�AD��BC=AP��BP�� ��AP=t��BP=6-t����t��6-t��=5��1��
���t1=1��t2=5�� ��t��ֵΪ1���5�룮


 �Ͻ�ƽ��У����ϵ�д�
�Ͻ�ƽ��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ԭ����һ��ʫ��̦���е�ʫ�䣺�����ղ��������ഺǡ����.̦������С��Ҳѧĵ����.����̦���Ļ���ֱ��ԼΪ0.0000084�ף�������0.0000084�ÿ�ѧ��������ʾΪ�� ��
A.8.4��10-5B.8.4��10-6C.84��10-7D.8.4��106
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������ˣ���Ϊ������ô�������������� ��
A. 2�� B. 3�� C. 4�� D. 2����4����0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Rt��ABC�У���ACB=90�㣬��CAB=30�����ֱ���AB��ACΪ�ߣ��������������ȱ���ABD�͵ȱ���ACE��
��1����ͼ1�������߶�BE��CD����֤��BE=CD��
��2����ͼ2������DE��AB�ڵ�F����֤��FΪDE�е㣮
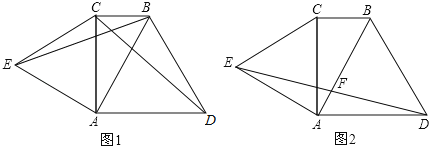
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���ABC�Ķ���A(��3��0)��B(0��3)��AD��BC��BC��D�㣬��y���������ڵ�E(0��t)
��1����t��1ʱ����C������ꣻ
��2����ͼ2�����ADO�Ķ�����
��3����ͼ3����֪��P(0��2)����PQ��PC��PQ��PC����Q������(�ú�t��ʽ�ӱ�ʾ)��
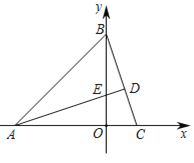
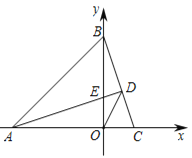
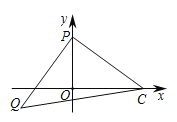
ͼ1 ͼ2 ͼ3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���ı��εı߳��ֱ���3��4��5��6����һ���������Ƶ��ı�����С�߳�Ϊ6������һ���ı��ε������________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У���ȷ���ǣ�������
A. ͬ������ˣ����Ų���
B. ������ˣ�����Ϊ������������������Ϊ��
C. ������ˣ�����Ϊ0��������������������һ��Ϊ0
D. ������ˣ���һ������ÿһ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ�������շѱ���ض��죬�����й涨����Ϊ6Ԫ��3ǧ��֮��ÿǧ��1.4Ԫ�������й涨����8Ԫ��3ǧ��֮��ÿǧ��1.2Ԫ��
��1����������������˳��2ǧ�ף�5ǧ��Ӧ���ij��ѣ�
��2��д���ڼ����˳����xǧ��ʱӦ���ij��ѣ�
��3������ʻ·�̳���3ǧ�ף�������l3ǧ��ʱ�����ڼ��ϡ���������������ij��������٣�
��4������������ڼ��Ϻͼ����˳�������ij�����ȣ��Թ�����������˳������ǧ�ף�ֱ��д���𰸣�����д���̣���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com