
【题目】已知,Rt△ABC中,∠ACB=90°,∠CAB=30°.分别以AB、AC为边,向三角形外作等边△ABD和等边△ACE.
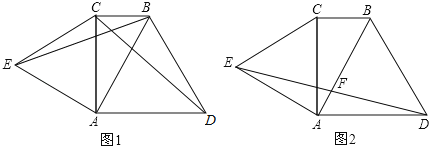
(1)如图1,连接线段BE、CD.求证:BE=CD;
(2)如图2,连接DE交AB于点F.求证:F为DE中点.
【答案】(1)证明见解析(2)证明见解析
【解析】此题考查了全等三角形的判定与性质,平行线的性质,以及等边三角形的性质,
(1)由△ABD和△ACE是等边三角形,根据等边三角形的性质得到AB=AD,AC=AE,∠DAB=∠EAC=60°,然后给∠DAB和∠EAC都加上∠BAC,得到∠DAC=∠BAE,利用“SAS“即可得到△DAC≌△BAE,最后根据全等三角形的对应边相等即可得证;
(2)作DG∥AE,交AB于点G,由等边三角形的∠EAC=60°,加上已知的∠CAB=30°得到∠FAE=90°,然后根据两直线平行内错角相等得到∠DGF=90°,再根据∠ACB=90°,∠CAB=30°,利用三角形的内角和定理得到∠ABC=60°,由等边三角形的性质也得到∠DBG=60°,从而得到两角的相等,再由DB=AB,利用“AAS”证得△DGB≌△ACB,根据全等三角形的对应边相等得到DG=AC,再由△AEC为等边三角形得到AE=AC,等量代换可得DG=AE,加上一对对顶角的相等和一对直角的相等根据“AAS”证得△DGF≌△EAF,最后根据全等三角形的对应边相等即可得证.
(1)∵△ABD和△ACE是等边三角形,
∴AB=AD,AC=AE,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,即∠DAC=∠BAE,
在△DAC和△BAE中,

∴△DAC≌△BAE(SAS),
∴DC=BE;
(2)如图,作DG∥AE,交AB于点G,

由∠EAC=60°,∠CAB=30°得:∠FAE=∠EAC+∠CAB=90°,
∴∠DGF=∠FAE=90°,
又∵∠ACB=90°,∠CAB=30°,
∴∠ABC=60°,
又∵△ABD为等边三角形,∠DBG=60°,DB=AB,
∴∠DBG=∠ABC=60°,
在△DGB和△ACB中,

∴△DGB≌△ACB(AAS),
∴DG=AC,
又∵△AEC为等边三角形,∴AE=AC,
∴DG=AE,
在△DGF和△EAF中,
∴△DGF≌△EAF(AAS),
∴DF=EF,即F为DE中点.


科目:初中数学 来源: 题型:
【题目】解方程-3x+5=2x-1,移项正确的是( )
A. 3x-2x=-1+5 B. -3x-2x=5-1
C. 3x-2x=-1-5 D. -3x-2x=-1-5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)甲、乙两家文具商店出售同样的毛笔和宣纸.毛笔每支18元,宣纸每张2元.甲商店推出的优惠方法为买一支毛笔送两张宣纸;乙商店的优惠方法为按总价的九折优惠.小丽想购买5支毛笔,宣纸x张(x≥5).
(1)若到甲商店购买,应付______ 元(用代数式表示);
(2)若到乙商店购买,应付______ 元(用代数式表示);
(3)若小丽要买宣纸10张,应选择哪家文具商店?若买100张呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+ax+a-2=0
(1)若该方程有一个实数根为1,求a的值及方程的另一实根.
(2)求证:不论a取何实数,该方程都有两个不相等的实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,某市共接待海内外游客约567000人次,将567000用科学记数法表示为( )
A. 567×103 B. 56.7×104 C. 5.67×105 D. 0.567×106
查看答案和解析>>
科目:初中数学 来源: 题型:
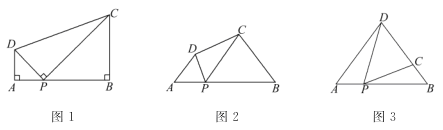
【题目】 (1)、问题:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.求证:AD·BC=AP·BP.
(2)、探究:如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
(3)、应用:请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=6,AD=BD=5.点P以每秒1个单位长度的速度,由点A 出发,沿边AB向点B运动,且满足∠DPC=∠A.设点P的运动时间为t(秒),当DC的长与△ABD底边上的高相等时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校围绕着“你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行了随机抽样调查,从而得到一组数据,如图是根据这组数据绘制的条形统计图,请结合统计图回答下列问题:

(1)该校对多少名学生进行了抽样调查?
(2)本次抽样调查中,最喜欢篮球活动的有多少人?占被调查人数的百分比是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
调查结果统计表
组别 | 分组(单位:元) | 人数 |
A | 0≤x<30 | 4 |
B | 30≤x<60 | 16 |
C | 60≤x<90 | a |
D | 90≤x<120 | b |
E | x≥120 | 2 |
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有__人,a+b=__,m=___;
(2)求扇形统计图中扇形C的圆心角度数;
(3)该校共有学生1000人,请估计每月零花钱的数额x在60≤x<120范围的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由长度为1个单位的若干小正方形组成的网格图中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)三角形ABC的面积为
(3)以AC为边作与△ABC全等的三角形(只要作出一个符合条件的三角形即可);
(4)在直线l上找一点P,使PB+PC的长最短.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com