
 如图,直线y1=2x+2与坐标轴交于A、B两点,与双曲线y2=$\frac{k}{x}$交于C、D两点,且DA=AB=BC.
如图,直线y1=2x+2与坐标轴交于A、B两点,与双曲线y2=$\frac{k}{x}$交于C、D两点,且DA=AB=BC.分析 (1)分别将x=0、y=0代入一次函数解析式中求出与之对应的y、x的值,由此即可得出点A、B的坐标;
(2)根据DA=AB=BC结合点A、B的坐标即可求出点D的坐标,再利用反比例函数图象上点的坐标特征即可得出结论.
解答 解:(1)当x=0时,y=2,
∴点A的坐标为(0,2);
当y=0时,有2x+2=0,解得:x=-1,
∴点B的坐标为(-1,0).
(2)∵DA=AB=BC,且A、B、C、D四点共线,
∴点A是线段BD的中点,
∵A(0,2),B(-1,0),
∴点D的坐标为(1,4).
∵点D在反比例函数y2=$\frac{k}{x}$的图象上,
∴k=1×4=4,
∴反比例函数的解析式为y2=$\frac{4}{x}$.
点评 本题考查了反比例函数与一次函数的交点问题、一次函数图象上点的坐标特征以及反比例函数图象上点的坐标特征,根据线段间的关系找出点D的坐标是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{b}$×$\frac{b}{a}$=1 | B. | $\frac{b}{a}$+$\frac{c}{a}$=$\frac{b+c}{a}$ | ||
| C. | ($\frac{a}{b}$)2=$\frac{({a}^{2}+2a)}{({b}^{2}+2b)}$ | D. | $\frac{a}{a}$=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
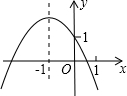 已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | -$\frac{4}{3}$ | D. | -$\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
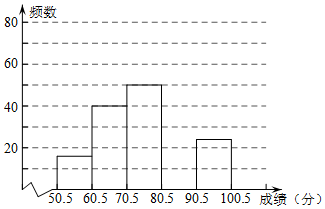 2015年3月30日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计.请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:
2015年3月30日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计.请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:| 分数段 | 频数 | 频率 |
| 50.5~60.5 | 16 | 0.08 |
| 60.5~70.5 | 40 | 0.2 |
| 70.5~80.5 | 50 | 0.25 |
| 80.5~90.5 | m | 0.35 |
| 90.5~100.5 | 24 | n |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5x-(x-2y)=5x-x+2y | B. | 2a+(-3a-b)=2a-3a-b | ||
| C. | -3(x+6)=-3x-6 | D. | -(x2+y2)=-x2-y2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com