Question

5．如图，抛物线y=ax²+bx+4交x轴于A、B两点，交y轴于点C，∠CBO=45°，OB=4OA．
（1）求抛物线的解析式；
（2）当P为抛物线上在第一象限图象上一点，设点P的横坐标为m，点D在线段CO上，CD=m，当△PCD是以CD为底的等腰三角形时，求P点坐标；
（3）在（2）的条件下，是否存在抛物线上一点Q，使∠PCB=∠APQ？若存在，求Q点的横坐标；若不存在请说明理由．

Answer 1

分析 （1）先确定出点C的坐标，进而得出点B，A坐标，最后用待定系数法求出抛物线解析式；
（2）先表示出点D坐标，进而得出E的坐标，由等腰三角形的性质得出PE⊥CD，从而得出点P坐标代入抛物线解析式即可；
（3）先判断出点A，D，P在同一条直线上，将∠BCP转化成∠FDP上，再分两种情况计算，①利用平行线即可得出直线PQ解析式，从而求出抛物线和直线PQ交点坐标即可，②利用等腰三角形的性质得出点N坐标，即可求出直线PQ'的解析式，从而求出抛物线和直线PQ'的交点坐标即可．

解答 解：（1）∵抛物线y=ax²+bx+4交y轴于点C，
∴C（0，4），
∴OC=4，
∵∠BOC=90°，∠CBO=45°，
∴OB=OC=4，
∴B（4，0），
∵OB=4OA，
∴OA=1，
∴A（-1，0），
∴$\left\{\begin{array}{l}{a-b+4=0}\\{16a+4b+4=0}\end{array}\right.$，
∴$\left\{\begin{array}{l}{a=-1}\\{b=3}\end{array}\right.$，
∴抛物线解析式为y=-x²+3x+4．
（2）如图1，过点P作PE⊥CD，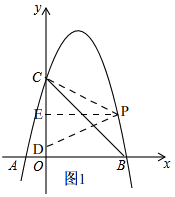

∵C（0，4），CD=m，
∴D（0，4-m），
∴CD的中点E坐标为（0，4-$\frac{m}{2}$），
∵△PCD是以CD为底的等腰三角形，
∴PE⊥CD，
∴P（m，4-$\frac{m}{2}$），
∵点P在抛物线y=-x²+3x+4上，
∴4-$\frac{m}{2}$=-m²+3m+4，
∴m=0（舍）或m=$\frac{7}{2}$，
∴D（0，$\frac{1}{2}$），P（$\frac{7}{2}$，$\frac{9}{4}$）；
即：P（$\frac{7}{2}$，$\frac{9}{4}$）；
（3）
存在点Q，
理由：如图2，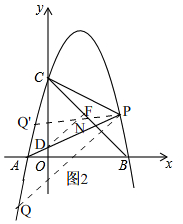

由（2）知，D（0，$\frac{1}{2}$），P（$\frac{7}{2}$，$\frac{9}{4}$）；
∵A（-1，0），
∴直线AP的解析式为y=$\frac{1}{2}$x+$\frac{1}{2}$，
∵D（0，$\frac{1}{2}$），
∴点A，D，P在同一条直线上，
过点D作DF⊥BC，则∠OCB=∠CDF=45°，
∴∠OCP=∠OCB+∠BCP=45°+∠BCP，
∵△PCD是以CD为底的等腰三角形，
∴∠OCP=∠CDP，
∴∠CDP=∠CDF+∠FDP=45°+∠FDP=45°+∠BCP，
∴∠FDP=∠BCP，
∵∠PCB=∠APQ，
∴∠FDP=∠APQ，
①当点Q在第三象限时，
过点P作PQ∥DF，则PQ和抛物线的交点就是Q，
∵B（4，0），C（0，4），
∴直线BC解析式为y=-x+4，
∵D（0，$\frac{1}{2}$），
∴直线DF的解析式为y=x+$\frac{1}{2}$，
∵P（$\frac{7}{2}$，$\frac{9}{4}$），
∴直线PQ解析式为y=x-$\frac{5}{4}$①，
由（1）知，抛物线解析式为y=-x²+3x+4②．
联立①②得，$\left\{\begin{array}{l}{x=\frac{7}{2}}\\{y=\frac{9}{4}}\end{array}\right.$（此种情况是点P坐标）或$\left\{\begin{array}{l}{x=-\frac{3}{2}}\\{y=-\frac{11}{4}}\end{array}\right.$，
∴Q（-$\frac{3}{2}$，-$\frac{11}{4}$），
∴Q点的横坐标为：-$\frac{3}{2}$，
②当点Q在第二象限是时，过点P作∠APQ'与DF相交于N，
∴ND=NP，
∴ND²=NP²，
∵直线DF解析式为y=x+$\frac{1}{2}$，
∴设点N（n，n+$\frac{1}{2}$），
∵D（0，$\frac{1}{2}$），P（$\frac{7}{2}$，$\frac{9}{4}$），
∴ND²=n²+（n+$\frac{1}{2}$-$\frac{1}{2}$）²=2n²，
NP²=（n-$\frac{7}{2}$）²+（n+$\frac{1}{2}$-$\frac{9}{4}$）²，
∴2n²=（n-$\frac{7}{2}$）²+（n+$\frac{1}{2}$-$\frac{9}{4}$）²，
∴n=$\frac{35}{24}$，
∴N（$\frac{35}{24}$，$\frac{47}{24}$），
∵P（$\frac{7}{2}$，$\frac{9}{4}$），
∴直线PQ'解析式为y=$\frac{1}{7}$x+$\frac{7}{4}$③，
联立②③得，$\left\{\begin{array}{l}{x=\frac{7}{2}}\\{y=\frac{9}{4}}\end{array}\right.$（此种情况是点P的坐标）或$\left\{\begin{array}{l}{x=-\frac{9}{14}}\\{y=\frac{255}{156}}\end{array}\right.$，
∴Q'（$-\frac{9}{14}$，$\frac{255}{156}$），
∴Q'点的横坐标为：-$\frac{9}{14}$，
即：Q点的横坐标为：-$\frac{3}{2}$和-$\frac{9}{14}$．

点评 此题是二次函数综合题，主要考查了待定系数法，等腰三角形的性质，平行线的性质，函数图象的交点坐标，解本题的关键是将∠BCP转化成∠FDP上，难点是判断出点A，D，P在同一条直线上，也是解（3）的突破口．