
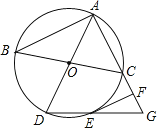
【题目】如图,△ABC内接于⊙O,AD与BC是⊙O的直径,延长线段AC至点G,使AG=AD,连接DG交⊙O于点E,EF∥AB交AG于点F.
(1)求证:EF与⊙O相切.
(2)若EF=2![]() ,AC=4,求扇形OAC的面积.
,AC=4,求扇形OAC的面积.
【答案】(1)见解析;(2)S扇形OAC=![]() .
.
【解析】
(1)连接OE,由条件知∠D=∠OED,证出∠OED=∠G,可得OE∥AG,证明∠OEF=180°∠AFE=90°,即OE⊥EF,则EF与⊙O相切.
(2)连接OE,过点O作OH⊥AC于点H,求出CH,OH的长,再求出OC的长,得出△AOC是等边三角形,则∠AOC=60°,可求出扇形OAC的面积.
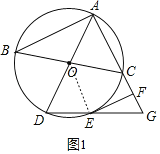
(1)证明:如图1,连接OE,
∵OD=OE,
∴∠D=∠OED,
∵AD=AG,
∴∠D=∠G,
∴∠OED=∠G,
∴OE∥AG,
∵BC是⊙O的直径,
∴∠BAC=90°,
∵EF∥AB,
∴∠BAF+∠AFE=180°,
∴∠AFE=90°,
∵OE∥AG,
∴∠OEF=180°﹣∠AFE=90°,
∴OE⊥EF,
∴EF与⊙O相切;
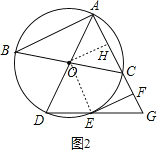
(2)解:如图2,连接OE,过点O作OH⊥AC于点H,
∵AC=4,
∴CH=![]() ,
,
∵∠OHF=∠HFE=∠OEF=90°,
∴四边形OEFH是矩形,
∴![]() ,
,
在Rt△OHC中,
OC=![]() =
=![]() =4,
=4,
∵OA=AC=OC=4,
∴△AOC是等边三角形,
∴∠AOC=60°,
∴S扇形OAC=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),他先测得留在墙壁上的影高为1.2m,又测得地面的影长为2.6m,请你帮她算一下,树高是( )

A、3.25m B、4.25m C、4.45m D、4.75m
查看答案和解析>>
科目:初中数学 来源: 题型:
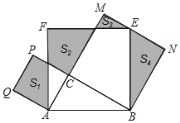
【题目】如图,Rt△ABC中,∠C=90°,AC=3,BC=4.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN,四块阴影部分的面积分别为S1、S2、S3、S4.则S1﹣S2+S3+S4等于( )
A. 4B. 6C. 8D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小西“过直线外一点作这条直线的垂线”的尺规作图过程.
已知:直线l及直线l外一点P.
求作:直线PQ,使得PQ⊥l.
做法:如图,
①在直线l的异侧取一点K,以点P为圆心,PK长为半径画弧,交直线l于点A,B;
②分别以点A,B为圆心,大于![]() AB的同样长为半径画弧,两弧交于点Q(与P点不重合);
AB的同样长为半径画弧,两弧交于点Q(与P点不重合);
③作直线PQ,则直线PQ就是所求作的直线.
根据小西设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵PA= ,QA= ,
∴PQ⊥l( )(填推理的依据).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(材料阅读)
我们曾解决过课本中的这样一道题目:
如图1,四边形ABCD是正方形,E为BC边上一点,延长BA至F,使AF=CE,连接DE,DF.……
提炼1:△ECD绕点D顺时针旋转90°得到△FAD;
提炼2:△ECD≌△FAD;
提炼3:旋转、平移、轴对称是图形全等变换的三种方式.
(问题解决)
(1)如图2,四边形ABCD是正方形,E为BC边上一点,连接DE,将△CDE沿DE折叠,点C落在G处,EG交AB于点F,连接DF.
可得:∠EDF= °;AF,FE,EC三者间的数量关系是 .
(2)如图3,四边形ABCD的面积为8,AB=AD,∠DAB=∠BCD=90°,连接AC.求AC的长度.
(3)如图4,在△ABC中,∠ACB=90°,CA=CB,点D,E在边AB上,∠DCE=45°.写出AD,DE,EB间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 是由抛物线
是由抛物线![]() :
:![]() 平移得到的,并且
平移得到的,并且![]() 的顶点为(1,-4)
的顶点为(1,-4)
(1)求![]() 的值;
的值;
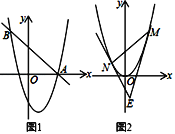
(2)如图1,抛物线C1与x轴正半轴交于点A,直线![]() 经过点A,交抛物线C1于另一点B.请你在线段AB上取点P,过点P作直线PQ∥y轴交抛物线C1于点Q,连接AQ.
经过点A,交抛物线C1于另一点B.请你在线段AB上取点P,过点P作直线PQ∥y轴交抛物线C1于点Q,连接AQ.
①若AP=AQ,求点P的坐标;
②若PA=PQ,求点P的横坐标.
(3)如图2,△MNE的顶点M、N在抛物线C2上,点M在点N右边,两条直线ME、NE与抛物线C2均有唯一公共点,ME、NE均与y轴不平行.若△MNE的面积为16,设M、N两点的横坐标分别为m、n,求m与n的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
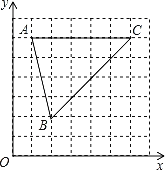
【题目】如图,坐标平面内,将△ABC放在每个小正方形的边长为l的网格中,点A(l,6),B(2,2),C(6,6),均为格点.
(1)①在B的下方找一格点D,使得∠ABC=∠CBD,画出图形,直接写出D的坐标 .
②P、Q为两格点,连PQ交BC于M,使得CM:BM=1:2,画出图形,并标出M的位置.
(2)E为一格点,作直线CE交y轴于N,若CE⊥AB,请用连线的方式找到N点,写出E的坐标 ,并画出图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
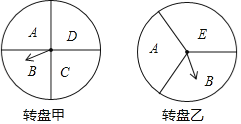
【题目】某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式,方式一:转动转盘甲,指针指向A区域时,所购买物品享受9折优惠、指针指向其它区域无优惠;方式二:同时转动转盘甲和转盘乙,若两个转盘的指针指向每个区域的字母相同,所购买物品享受8折优惠,其它情况无优惠.在每个转盘中,指针指向每个区城的可能性相同(若指针指向分界线,则重新转动转盘)
(1)若顾客选择方式一,则享受9折优惠的概率为多少;
(2)若顾客选择方式二,请用树状图或列表法列出所有可能,并求顾客享受8折优惠的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com