
【题目】已知抛物线![]() :
:![]() 是由抛物线
是由抛物线![]() :
:![]() 平移得到的,并且
平移得到的,并且![]() 的顶点为(1,-4)
的顶点为(1,-4)
(1)求![]() 的值;
的值;
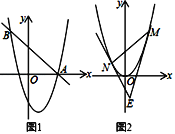
(2)如图1,抛物线C1与x轴正半轴交于点A,直线![]() 经过点A,交抛物线C1于另一点B.请你在线段AB上取点P,过点P作直线PQ∥y轴交抛物线C1于点Q,连接AQ.
经过点A,交抛物线C1于另一点B.请你在线段AB上取点P,过点P作直线PQ∥y轴交抛物线C1于点Q,连接AQ.
①若AP=AQ,求点P的坐标;
②若PA=PQ,求点P的横坐标.
(3)如图2,△MNE的顶点M、N在抛物线C2上,点M在点N右边,两条直线ME、NE与抛物线C2均有唯一公共点,ME、NE均与y轴不平行.若△MNE的面积为16,设M、N两点的横坐标分别为m、n,求m与n的数量关系.
【答案】(1)![]() ;(2)①P点坐标为
;(2)①P点坐标为![]() ;②P点横坐标为﹣
;②P点横坐标为﹣![]() ;(3)m﹣n=4.
;(3)m﹣n=4.
【解析】
(1)抛物线![]() :
:![]() 是由抛物线
是由抛物线![]() :
:![]() 平移得到的,求出
平移得到的,求出 ![]() ,
,
由抛物线![]() 的顶点为(1,-4),即可求出b、c的值;
的顶点为(1,-4),即可求出b、c的值;
(2)由直线![]() 经过点A,求出b的值,从而求出直线和抛物线的解析式,设P(t,﹣
经过点A,求出b的值,从而求出直线和抛物线的解析式,设P(t,﹣![]() t+4),根据PQ∥y轴,推出Q(t,t2﹣2t﹣3),分两种情况:①当AP=AQ时,②当AP=PQ时,列出关于t的方程,即可求解;
t+4),根据PQ∥y轴,推出Q(t,t2﹣2t﹣3),分两种情况:①当AP=AQ时,②当AP=PQ时,列出关于t的方程,即可求解;
(3)设经过![]() 的直线解析式为y=k(x﹣m)+m2,直线ME与
的直线解析式为y=k(x﹣m)+m2,直线ME与![]() 的方程联立得到方程组,由直线ME与
的方程联立得到方程组,由直线ME与![]() 有唯一公共点,得到k=2m,直线ME的解析式为y=2mx﹣m2,同理可求直线NE的解析式为y=2nx﹣n2,求得E
有唯一公共点,得到k=2m,直线ME的解析式为y=2mx﹣m2,同理可求直线NE的解析式为y=2nx﹣n2,求得E![]() .过E作直线
.过E作直线![]() ∥x轴,分别过M,N作
∥x轴,分别过M,N作![]() 的垂线,垂足为C,D,根据
的垂线,垂足为C,D,根据![]() ,列出关于m,n的方程,即可求解.
,列出关于m,n的方程,即可求解.
(1)∵抛物线![]() :
:![]() 是由抛物线
是由抛物线![]() :
:![]() 平移得到的,
平移得到的,
∴![]() ,
,
∵抛物线![]() 的顶点为(1,-4)
的顶点为(1,-4)
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
(2)y=(x﹣1)2﹣4与x轴正半轴的交点A(3,0),
∵直线y=﹣![]() x+b经过点A,
x+b经过点A,
∴b=4,
∴y=﹣![]() x+4,
x+4,
﹣![]() x+4=(x﹣1)2﹣4,
x+4=(x﹣1)2﹣4,
∴x=3或x=﹣![]() ,
,
∴B(﹣![]() ,
,![]() ),
),
设P(t,﹣![]() t+4),且﹣
t+4),且﹣![]() <t<3,
<t<3,
∵PQ∥y轴,
∴Q(t,t2﹣2t﹣3),
①当AP=AQ时,
|4﹣![]() t|=|t2﹣2t﹣3|,
t|=|t2﹣2t﹣3|,
则有﹣4+![]() t=t2﹣2t﹣3,
t=t2﹣2t﹣3,
∴t=![]() ,
,
∴P点坐标为![]()
②当AP=PQ时,
PQ=t2+![]() t+7,PA=
t+7,PA=![]() (3﹣t),
(3﹣t),
∴-t2+![]() t+7=
t+7=![]() (3﹣t),
(3﹣t),
∴t=﹣![]() ;
;
∴P点横坐标为﹣![]()
(3)设经过![]() 的直线解析式为y=k(x﹣m)+m2,
的直线解析式为y=k(x﹣m)+m2,
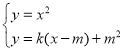 ,则有x2﹣kx+km﹣m2=0,
,则有x2﹣kx+km﹣m2=0,
∵直线ME与![]() 有唯一公共点,
有唯一公共点,
∴△=k2﹣4km+4m2=(k﹣2m)2=0,
∴k=2m,直线ME的解析式为y=2mx﹣m2,
同理可求直线NE的解析式为y=2nx﹣n2,
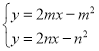
∴E![]() ,
,
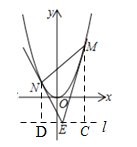
如图,过E作直线![]() ∥x轴,分别过M,N作
∥x轴,分别过M,N作![]() 的垂线,垂足为C,D,
的垂线,垂足为C,D,
![]()
∴![]() [(n2﹣mn)+(m2﹣mn)]×(m﹣n)﹣
[(n2﹣mn)+(m2﹣mn)]×(m﹣n)﹣![]() (n2﹣mn)×(
(n2﹣mn)×(![]() ﹣n)﹣
﹣n)﹣![]() (m2﹣mn)×(m﹣
(m2﹣mn)×(m﹣![]() )=16,
)=16,
∴(m﹣n)3=64,
∴m﹣n=4


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
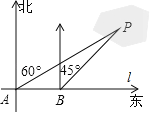
【题目】为了计算湖中小岛上凉亭P到岸边公路l的距离,某数学兴趣小组在公路l上的点A处,测得凉亭P在北偏东60°的方向上;从A处向正东方向行走200米,到达公路l上的点B处,再次测得凉亭P在北偏东45°的方向上,如图所示.求凉亭P到公路l的距离.(结果保留整数,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点P、D分别在边BC、AC上,PA⊥AB,垂足为点A,DP⊥BC,垂足为点P,![]() .
.
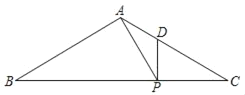
(1)求证:∠APD=∠C;
(2)如果AB=3,DC=2,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
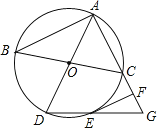
【题目】如图,△ABC内接于⊙O,AD与BC是⊙O的直径,延长线段AC至点G,使AG=AD,连接DG交⊙O于点E,EF∥AB交AG于点F.
(1)求证:EF与⊙O相切.
(2)若EF=2![]() ,AC=4,求扇形OAC的面积.
,AC=4,求扇形OAC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)若点D在y轴负半轴上,且满足S△COD=![]() S△BOC,求点D的坐标.
S△BOC,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示8×7的正方形网格中,A(2,0),B(3,2),C(4,2),请按要求解答下列问题:

(1)将△ABO向右平移4个单位长度得到△A1B1O1,请画出△A1B1O1并写出点A1的坐标;
(2)将△ABO绕点C(4,2)顺时针旋转90°得到△A2B2O2,请画出△A2B2O2并写出点A2的坐标;
(3)将△A1B1O1绕点Q旋转90°可以和△A2B2O2完全重合,请直接写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
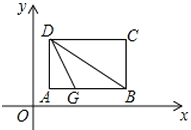
【题目】如图,把矩形纸片ABCD置于直角坐标系中,AB∥x轴,BC∥y轴,AB=4,BC=3,点B(5,1)翻折矩形纸片使点A落在对角线DB上的H处得折痕DG.
(1)求AG的长;
(2)在坐标平面内存在点M(m,-1)使AM+CM最小,求出这个最小值;
(3)求线段GH所在直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从宁海县到某市,可乘坐普通列车或高铁,已知高铁的行驶路程与普通列车的行驶路程之和是920千米,而普通列车的行驶路程是高铁的行驶路程的1.3倍.
(1)求普通列车的行驶路程;
(2)若高铁的平均速度(千米/时)是普通列车的平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com