
【题目】已知AB//CD,点E为平面内一点,BE⊥CE于E
(1)如图1,请直接写出∠ABE和∠DCE之间的数量关系
(2)如图2,过点E作EF⊥CD,垂足为F,求证:∠CEF=∠ABE
(3)如图3,在(2)的条件下,作EG平分∠CEF,交DF于点G,作ED平分∠BEF,交CD于D,连接BD,若∠DBE+∠ABD=180°,且∠BDE=3∠GEF,求∠BEG的度数.

【答案】(1)∠ECD=90°+∠ABE;(2)见解析;(3)105°
【解析】
(1)如图1中,从BE交DC的延长线于H.利用三角形内角和定理即可证明;
(2)只要证明∠CEF与∠CEM互余,∠BEM与∠CEM互余,可得∠CEF=∠BEM即可解决问题;
(3)如图3中,设∠GEF=![]() ,∠EDF=
,∠EDF=![]() .想办法构建方程求出
.想办法构建方程求出![]() 即可解决问题;
即可解决问题;
(1)结论:∠ECD=90°+∠ABE.
理由:如图1中,延长BE交DC的延长线于H.

∵AB∥CH,
∴∠ABE=∠H,
∵BE⊥CE,
∴∠CEH=90°,
∴∠ECH=180°∠CEH∠H=180°90°∠H=90°∠H,
∴∠ECD=180°∠ECH=180°(90°∠H)=90°+∠H,
∴∠ECD=90°+∠ABE.
(2)如图2中,作EM∥CD,

∵EM∥CD,CD∥AB,
∴AB∥CD∥EM,
∴∠BEM=∠ABE,∠F+∠FEM=180°,
∵EF⊥CD,
∴∠F=90°,
∴∠FEM=90°,
∴∠CEF与∠CEM互余,
∵BE⊥CE,
∴∠BEC=90°,
∴∠BEM与∠CEM互余,
∴∠CEF=∠BEM,
∴∠CEF=∠ABE.
(3)如图3中,设∠GEF=![]() ,∠EDF=
,∠EDF=![]() .
.

∴∠BDE=3∠GEF=3![]() ,
,
∵EG平分∠CEF,
∴∠CEF=2∠FEG=2![]() ,
,
∴∠ABE=∠CEF=2![]() ,
,
∵AB∥CD∥EM,
∴∠MED=∠EDF=![]() ,∠KBD=∠BDF=3
,∠KBD=∠BDF=3![]() +
+![]() ,∠ABD+∠BDF=180°,
,∠ABD+∠BDF=180°,
∴∠BED=∠BEM+∠MED=2![]() +
+![]() ,
,
∵ED平分∠BEF,
∴∠BED=∠FED=2![]() +
+![]() ,
,
∴∠DEC=![]() ,
,
∵∠BEC=90°,
∴2![]() +2
+2![]() =90°,
=90°,
∵∠DBE+∠ABD=180°,∠ABD+∠BDF=180°,
∴∠DBE=∠BDF=∠BDE+∠EDF=3![]() +
+![]() ,
,
∵∠ABK=180°,
∴∠ABE+∠B=DBE+∠KBD=180°,
即2![]() +(3
+(3![]() +
+![]() )+(3α+
)+(3α+![]() )=180°,
)=180°,
∴6![]() +(2
+(2![]() +2
+2![]() )=180°,
)=180°,
∴![]() =15°,
=15°,
∴∠BEG=∠BEC+∠CEG=90°+15°=105°.


科目:初中数学 来源: 题型:
【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.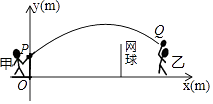
(1)当a=﹣ ![]() 时,①求h的值;
时,①求h的值;
②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为 ![]() m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个长为4,宽为3,高为12矩形牛奶盒,从上底一角的小圆孔插入一根到达底部的直吸管,吸管在盒内部分a的长度范围是(牛奶盒的厚度、小圆孔的大小及吸管的粗细均忽略不计)( )

A. 5≤a≤12B. 12≤a≤3![]()
C. 12≤a≤4![]() D. 12≤a≤13
D. 12≤a≤13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:CD是经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.

(1)若直线CD经过∠BCA的内部,且E,F在射线CD上.
①如图1,若∠BCA=90°,∠α=90°,则BE CF;
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件 ,使①中的结论仍然成立,并说明理由;
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图所示,某公路一侧有A、B两个送奶站,C为公路上一供奶站,CA和CB为供奶路线,现已测得AC=8km,BC=15km,AB=17km,∠1=30°,若有一人从C处出发,沿公路边向右行走,速度为2.5km/h,问:多长时间后这个人距B送奶站最近?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同),其中白球有2个,黄球有1个,再从中任意摸出1个球是白球的概率为 ![]() .
.
(1)试求袋中蓝球的个数;
(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法表示两次摸到球的所有可能结果,并求两次摸到的球都是白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( ) 
A.45°
B.54°
C.40°
D.50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,A(m,n+2),B(m+4,n).
(1)当m=2,n=2时,
①如图1,连接AO、BO,求三角形ABO的面积;
②如图2,在y轴上是否存在点P,使三角形PAB的面积等于8,若存在,求P点坐标;若不存在,请说明理由;
(2)如图3,过A、B两点作直线AB,当直线AB过y轴上点Q(0,3)时,试求出m,n的关系式.
(温情提示:(a+b)×(c+d)=ac+ad+bc+bd)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一块正方形ABCD木板上要贴三种不同的墙纸,正方形EFCG部分贴A型墙纸,△ABE部分贴B型墙纸,其余部分贴C型墙纸.A型、B型、C型三种墙纸的单价分别为每平方米60元、80元、40元.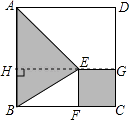
(1)探究1:如果木板边长为1米,FC= ![]() 米,则一块木板用墙纸的费用需元;
米,则一块木板用墙纸的费用需元;
(2)探究2:如果木板边长为2米,正方形EFCG的边长为x米,一块木板需用墙纸的费用为y元,
①用含x的代数式表示y(写过程).
②如果一块木板需用墙纸的费用为225元,求正方形EFCG的边长为多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com