
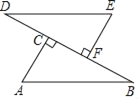
【题目】如图,D、C、F、B四点在一条直线上,AB=DE,AC⊥BD,EF⊥BD,垂足分别为点C、点F,CD=BF.
求证:(1)△ABC≌△EDF;
(2)AB∥DE.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)先根据AC⊥BD,EF⊥BD,可得△ABC和△EDF为直角三角形,由CD=BF,
可得CF+BF=CF+CD,即BC=DF,在Rt△ABC和Rt△EDF中,由![]() 可判定Rt△ABC≌Rt△EDF(HL),
可判定Rt△ABC≌Rt△EDF(HL),
(2)由(1)可知△ABC≌△EDF,根据全等三角形的性质可得:∠B=∠D,根据平行线的判定定理可得:AB∥DE.
(1)∵AC⊥BD,EF⊥BD,
∴△ABC和△EDF为直角三角形,
∵CD=BF,
∴CF+BF=CF+CD,即BC=DF,
在Rt△ABC和Rt△EDF中,
![]() ,
,
∴Rt△ABC≌Rt△EDF(HL),
(2)由(1)可知△ABC≌△EDF,
∴∠B=∠D,
∴AB∥DE.


科目:初中数学 来源: 题型:
【题目】一食堂需要购买盒子存放食物,盒子有A、B两种型号,单个盒子的容量和价格如表格所示.现有15升食物需要存放且要求每个盒子都要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性每个返还现金1.5元,则该食堂购买盒子所需的最少费用是 .
型号 | A | B |
单个盒子容量(升) | 2 | 3 |
单价(元) | 5 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组乘汽车从![]() 地出发,在东西走向的马路上检修线路,如果规定向东行驶为正,一天中七个检修点的行驶记录如下(单位:
地出发,在东西走向的马路上检修线路,如果规定向东行驶为正,一天中七个检修点的行驶记录如下(单位:![]() ):
):
-4,+7,-9,+8,+6,-4,-3.
(1)收工时汽车共行驶了多少千米?
(2)收工时,汽车距![]() 地多远?
地多远?
(3)在检修时,第几个检修点离![]() 地最远,最远距离是多少?
地最远,最远距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在下列各图中,点O为直线AB上一点,∠AOC=60°,直角三角板的直角顶点放在点处.
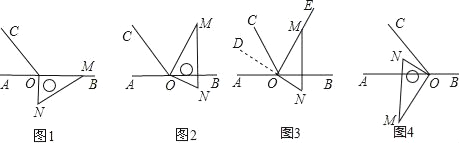
(1)如图1,三角板一边OM在射线OB上,另一边ON在直线AB的下方,则∠BOC的度数为 °,∠CON的度数为 °;
(2)如图2,三角板一边OM恰好在∠BOC的角平分线OE上,另一边ON在直线AB的下方,此时∠BON的度数为 °;
(3)请从下列(A),(B)两题中任选一题作答.
我选择: .
(A)在图2中,延长线段NO得到射线OD,如图3,则∠AOD的度数为 °;∠DOC与∠BON的数量关系是∠DOC ∠BON(填“>”、“=”或“<”);
(B)如图4,MN⊥AB,ON在∠AOC的内部,若另一边OM在直线AB的下方,则∠COM+∠AON的度数为 °;∠AOM﹣∠CON的度数为 °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读后解决问题:
在“15.3分式方程”一课的学习中,老师提出这样的一个问题:如果关于x的分式方程![]() 的解为正数,那么a的取值范围是什么?
的解为正数,那么a的取值范围是什么?
经过交流后,形成下面两种不同的答案:
小明说:解这个关于x的分式方程,得到方程的解为x=a﹣2.
因为解是正数,可得a﹣2>0,所以a>2.
小强说:本题还要必须a≠3,所以a取值范围是a>2且a≠3.
(1)小明与小强谁说的对,为什么?
(2)关于x的方程![]() 有整数解,求整数m的值.
有整数解,求整数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个底面直径为 5cm,高为 18cm 的圆柱形瓶内装满水,再将瓶内得水倒入一个底面直径为 6cm,高为 10cm 的圆柱形玻璃杯中,能否完全装下? 若装不下,那么瓶内水面还有多高? 若未能装满,求杯内水面离杯口的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E、F.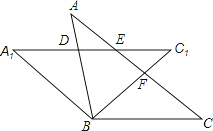
(1)求证:△BCF≌△BA1D.
(2)当∠C=α度时,判定四边形A1BCE的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若数 a,b 在数轴上的位置如图所示,则下列各式中一定成立的是( )
![]()
A. ﹣a>b B. a+b>0 C. a﹣b>a+b D. |a|+|b|<|a+b|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com