
【题目】已知,在下列各图中,点O为直线AB上一点,∠AOC=60°,直角三角板的直角顶点放在点处.
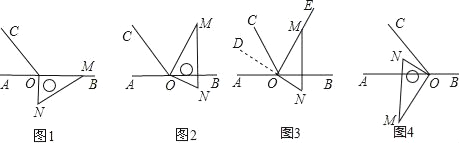
(1)如图1,三角板一边OM在射线OB上,另一边ON在直线AB的下方,则∠BOC的度数为 °,∠CON的度数为 °;
(2)如图2,三角板一边OM恰好在∠BOC的角平分线OE上,另一边ON在直线AB的下方,此时∠BON的度数为 °;
(3)请从下列(A),(B)两题中任选一题作答.
我选择: .
(A)在图2中,延长线段NO得到射线OD,如图3,则∠AOD的度数为 °;∠DOC与∠BON的数量关系是∠DOC ∠BON(填“>”、“=”或“<”);
(B)如图4,MN⊥AB,ON在∠AOC的内部,若另一边OM在直线AB的下方,则∠COM+∠AON的度数为 °;∠AOM﹣∠CON的度数为 °.
【答案】(1)120;150.(2)30°.(3)A(或B);30;=;150;30.
【解析】
试题(1)利用两角互补,即可得出结论;
(2)根据OM平分∠BOC,可得出∠BOM=60°,由∠BOM+∠BON=∠MON=90°可求得∠BON的度数;
(3)根据直角三角板MON各角的度数以及图中各角的关系即能得出结论.
解:(1)∵∠AOC=60°,∠BOC与∠AOC互补,∠AON=90°
∴∠BOC=180°﹣60°=120°,∠CON=∠AOC+∠AON=60°+90°.
故答案为:120;150.
(2)∵三角板一边OM恰好在∠BOC的角平分线OE上,∠BOC=120°,
∴∠BOM=![]() ∠BOC=60°,
∠BOC=60°,
又∵∠MON=∠BOM+∠BON=90°,
∴∠BON=90°﹣60°=30°.
故答案为:30°.
(3)(A)∵∠AOD=∠BON(对顶角),∠BON=30°,
∴∠AOD=30°,
又∵∠AOC=60°,
∴∠DOC=∠AOC﹣∠AOD=60°﹣30°=30°=∠BON.
(B)∵MN⊥AB,
∴∠AON与∠MNO互余,
∵∠MNO=60°(三角板里面的60°角),
∴∠AON=90°﹣60°=30°,
∵∠AOC=60°,150
∴∠CON=∠AOC﹣∠AON=60°﹣30°=30°,
∴∠COM+∠AON=∠MON+2∠CON=90°+2×30°=150°,
∠AOM﹣∠CON=∠MON﹣2∠CON=90°﹣2×30°=30°.
故答案为:A(或B);30;=;150;30.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】某校甲、乙两班分别有一男生和一女生共4名学生报名竞选校园广播播音员.
(1)若从甲、乙两班报名的学生中分别随机选1名学生,则所选的2名学生性别相同的概率是多少?
(2)若从报名的4名学生中随机选2名,求这2名学生来自同一班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.

(1)求证:AE=2CE;
(2)连接CD,请判断△BCD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“爱我永州”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:
甲:8、7、9、8、8
乙:7、9、6、9、9
则下列说法中错误的是( )
A.甲、乙得分的平均数都是8
B.甲得分的众数是8,乙得分的众数是9
C.甲得分的中位数是9,乙得分的中位数是6
D.甲得分的方差比乙得分的方差小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个长方形运动场被分隔成![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 共
共![]() 个区,
个区, ![]() 区是边长为
区是边长为![]() 的正方形,
的正方形, ![]() 区是边长为
区是边长为![]() 的正方形.
的正方形.
(1)列式表示每个![]() 区长方形场地的周长,并将式子化简;
区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果![]() ,
, ![]() ,求整个长方形运动场的面积.
,求整个长方形运动场的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产了台数相同A型、B型两种单价不同的计算机,B型机的单价比A型机的便宜0.24万元,已知A型机总价值120万元,B型计算机总价值为80万元,求A型、B型两种计算机的单价,设A型计算机的单价是x万元,可列方程_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
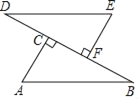
【题目】如图,D、C、F、B四点在一条直线上,AB=DE,AC⊥BD,EF⊥BD,垂足分别为点C、点F,CD=BF.
求证:(1)△ABC≌△EDF;
(2)AB∥DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE⊥AC于E,CF⊥AB于F,AE=AF,BE与CF交于点D,则:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.以上结论正确的是( )
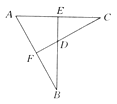
A. ① B. ② C. ①② D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把正整数1,2,3,4,…,2 009排列成如图所示的一个表.
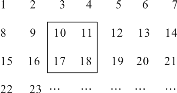
(1)用一正方形在表中随意框住4个数,把其中最小的数记为x,另三个数用含x的式子表示出来,从小到大依次是__ __,__ __,__ __;
(2)在(1)前提下,当被框住的4个数之和等于416时,x的值是多少?
(3)在(1)前提下,被框住的4个数之和能否等于622?如果能,请求出此时x的值;如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com