练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在“爱我永州”中学生演讲比赛中，五位评委分别给甲、乙两位选手的评分如下：
    甲：8、7、9、8、8
    乙：7、9、6、9、9
    则下列说法中错误的是（　　）
    A.甲、乙得分的平均数都是8
    B.甲得分的众数是8，乙得分的众数是9
    C.甲得分的中位数是9，乙得分的中位数是6
    D.甲得分的方差比乙得分的方差小

    【答案】C
    【解析】解：A、 = =8， = =8，故此选项正确；
    B、甲得分次数最多是8分，即众数为8分，乙得分最多的是9分，即众数为9分，故此选项正确；
    C、∵甲得分从小到大排列为：7、8、8、8、9，∴甲的中位数是8分；
    ∵乙得分从小到大排列为：6、7、9、9、9，∴乙的中位数是9分；故此选项错误；
    D、∵ = ×[（8﹣8）2+（7﹣8）2+（9﹣8）2+（8﹣8）2+（8﹣8）2]= ×2=0.4， = ×[（7﹣8）2+（9﹣8）2+（6﹣8）2+（9﹣8）2+（9﹣8）2]= ×8=1.6，∴ ＜ ，故D正确；
    故选：C．
    分别求出甲、乙的平均数、众数、中位数及方差可逐一判断．本题主要考查平均数、众数、中位数及方差，熟练掌握这些统计量的意义及计算公式是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

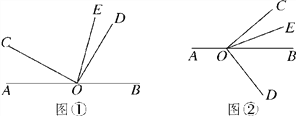
    【题目】已知O是直线AB上的一点，∠COD是直角，OE平分∠BOC.

    （1）如图①，若∠AOC＝30°，求∠DOE的度数；

    （2）在图①中，若∠AOC＝，直接写出∠DOE的度数（用含的代数式表示）；

    （3）将图①中的∠DOC绕顶点O顺时针旋转至图②的位置，探究∠AOC和∠DOE的度数之间的关系，写出你的结论，并说明理由；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若十位上的数字比个位上的数字、百位上的数字都大的三位数叫做中高数，如796就是一个“中高数”．若一个三位数的十位上数字为7，且从4、5、6、8中随机选取两数，与7组成“中高数”，那么组成“中高数”的概率是多少？（请用“画树状图”或“列表”等方法写出分析过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】A、B两地相距70千米，甲从A地出发，每小时行15千米，乙从B地出发，每小时行20千米．

    （1）若两人同时出发，相向而行，则经过几小时两人相遇？

    （2）若甲在前，乙在后，两人同时同向而行，则几小时后乙追上甲？

    （3）若两人同时出发，相向而行，则几小时后两人相距10千米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某检修小组乘汽车从地出发，在东西走向的马路上检修线路，如果规定向东行驶为正，一天中七个检修点的行驶记录如下（单位：）：

    －4，＋7，－9，＋8，＋6，－4，－3．

    （1）收工时汽车共行驶了多少千米？

    （2）收工时，汽车距地多远？

    （3）在检修时，第几个检修点离地最远，最远距离是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，∠DAC是△ABC的一个外角．

    实验与操作：根据要求进行尺规作图，并在图中标明相应字母（保留作图痕迹，不写作法）

    （1）作∠DAC的平分线AM；

    （2）作线段AC的垂直平分线，与AM交于点F，与BC边交于点E，连接AE、CF

    探究与猜想：若∠BAE=36°，求∠B的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，在下列各图中，点O为直线AB上一点，∠AOC＝60°，直角三角板的直角顶点放在点处．

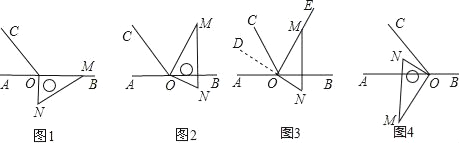
    （1）如图1，三角板一边OM在射线OB上，另一边ON在直线AB的下方，则∠BOC的度数为　 　°，∠CON的度数为　 　°；

    （2）如图2，三角板一边OM恰好在∠BOC的角平分线OE上，另一边ON在直线AB的下方，此时∠BON的度数为　 　°；

    （3）请从下列（A），（B）两题中任选一题作答．

    我选择：　 　．

    （A）在图2中，延长线段NO得到射线OD，如图3，则∠AOD的度数为　 　°；∠DOC与∠BON的数量关系是∠DOC　 　∠BON（填“＞”、“＝”或“＜”）；

    （B）如图4，MN⊥AB，ON在∠AOC的内部，若另一边OM在直线AB的下方，则∠COM+∠AON的度数为　 　°；∠AOM﹣∠CON的度数为　 　°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读后解决问题：

    在“15.3分式方程”一课的学习中，老师提出这样的一个问题：如果关于x的分式方程的解为正数，那么a的取值范围是什么？

    经过交流后，形成下面两种不同的答案：

    小明说：解这个关于x的分式方程，得到方程的解为x=a﹣2．

    因为解是正数，可得a﹣2＞0，所以a＞2．

    小强说：本题还要必须a≠3，所以a取值范围是a＞2且a≠3．

    （1）小明与小强谁说的对，为什么？

    （2）关于x的方程有整数解，求整数m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：﹣14+ sin60°+（ ）﹣2﹣（ ）0 ．

    查看答案和解析>>

    同步练习册答案